��Ŀ����
4��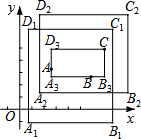 ��ƽ��ֱ������ϵxOy�У�������������A��B��C���������¶��壺
��ƽ��ֱ������ϵxOy�У�������������A��B��C���������¶��壺�����ε��κ�һ���߾���ij��������ƽ�У���A��B��C���㶼�ھ��ε��ڲ���߽��ϣ���Ƹþ���Ϊ��A��B��C�����Ӿ��Σ���A��B��C���������Ӿ����У������С�ľ��γ�Ϊ��A��B��C��������Ӿ��Σ����磬ͼ1�еľ���A1B1C1D1��A2B2C2D2��A3B3CD3���ǵ�A��B��C�����Ӿ��Σ�����A3B3CD3�ǵ�A��B��C��������Ӿ��Σ�
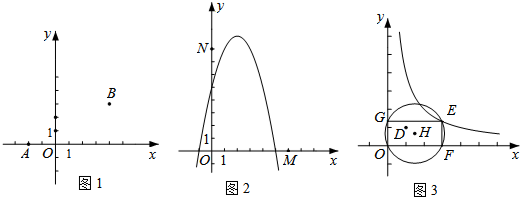
��1����ͼ1����֪A��-2��0����B��4��3����C��0��t����
����t=2�����A��B��C��������Ӿ��ε����Ϊ18��
������A��B��C��������Ӿ��ε����Ϊ24����t��ֵΪ4��-1��
��2����ͼ2����֪��M��6��0����N��0��8����P��x��y����������y=-x2+4x+5��һ�㣬���M��N��P��������Ӿ����������Сֵ���Լ���ʱ��P�ĺ�����x��ȡֵ��Χ��
��3����ͼ3����֪��D��1��1����E��m��n���Ǻ���y=$\frac{4}{x}$��x��0����ͼ����һ�㣬����OFEG�ǵ�O��D��E��һ�������С��������Ӿ��Σ���H�Ǿ���OFEG�����Բ����ֱ��д����H�İ뾶r��ȡֵ��Χ��
���� ��1��������������Ӿ��εĶ�����⼴�ɣ�������������Ӿ��εĶ�����⼴�ɣ�
��2�������M��N��P��������Ӿ��Σ��������С�����������������y�ἰ���εĽ��㼴�������M��N��P��������Ӿ����������Сֵʱ��P�ĺ�����x��ȡֵ��Χ��
��3�����OD���ڵ�ֱ�߽�˫�����ڵ�E������OFEG�ǵ�O��D��E��һ�������С��������Ӿ���ʱ��H�İ뾶������E��������Ϊ1ʱ����OFEG�ǵ�O��D��E��һ�������С��������Ӿ���ʱ��H�İ뾶���ɣ�
��� �⣺��1������ͼ1��
��A��-2��0����B��4��3����C��0��2����
���A��B��C��������Ӿ��ε����Ϊ[4-��-2��]��3=18��
�ʴ�Ϊ��18��
����ͼ2��
�ߵ�A��B��C��������Ӿ��ε����Ϊ24��
��A��-2��0����B��4��3����C��0��4����A��-2��0����B��4��3����C��0��-1����
��t=4��t=-1��
�ʴ�Ϊ��4��-1��
��2����ͼ3����M����x��Ĵ������N�㴹ֱ��y���ֱ�߽��ڵ�Q����Pλ�ھ���OMQN�ڲ���߽�ʱ������OMQN�ǵ�M��N��P��������Ӿ��Σ��������С��
��S����OMQN=OM•ON=6��8=48��
���M��N��P��������Ӿ����������СֵΪ48��
������y=-x2+4x+5��y�ύ�ڵ�T��0��5����
��y=0����-x2+4x+5=0��
��� x=-1���ᣩ����x=5��
��y=8����=-x2+4x+5=8��
��� x=1����x=3��
��0��x��1����3��x��5��
��3����ͼ4��OD���ڵ�ֱ�߽�˫�����ڵ�E������OFEG�ǵ�O��D��E��һ�������С��������Ӿ��Σ�
�ߵ�D��1��1����
��OD���ڵ�ֱ�߱���ʽΪy=x��
���E��������2��2��
��OE=2$\sqrt{2}$��
���H�İ뾶r=$\sqrt{2}$��
��ͼ5��
�ߵ���E��������Ϊ1ʱ��1=$\frac{x}{4}$�����x=4��
��OE=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$��
���H�İ뾶r=$\frac{\sqrt{17}}{2}$��
��$\sqrt{2}��r��\frac{{\sqrt{17}}}{2}$��
���� ������Ҫ�����˶��κ������ۺ��⣬�漰������꣬�����μ������ε������˫���ߵ�֪ʶ������Ĺؼ���������Ӿ��εĶ��壮

| ���� | һ | �� | �� | �� | �� | ���� | ��ƽ��������� |
| ������� | 1�� |  | -2�� | 0�� | 4�� |  | 1�� |
| A�� | 2��2 | B�� | 2��4 | C�� | 4��2 | D�� | 4��4 |
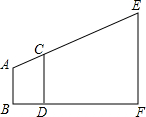 ��ͼ�����ñ�˲���¥�ߣ���֪AB=180m�����CD=240m��BD=30m��DF=420m����¥��EF=1080m��
��ͼ�����ñ�˲���¥�ߣ���֪AB=180m�����CD=240m��BD=30m��DF=420m����¥��EF=1080m�� ��ͼ��ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O����ABD=2��DBC��AE��BD��
��ͼ��ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O����ABD=2��DBC��AE��BD��