题目内容
15.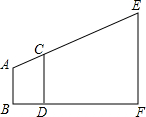 如图,利用标杆测量楼高,已知AB=180m,标杆CD=240m,BD=30m,DF=420m,则楼高EF=1080m.
如图,利用标杆测量楼高,已知AB=180m,标杆CD=240m,BD=30m,DF=420m,则楼高EF=1080m.
分析 根据题意过点A作AM⊥EF,垂足为M,交DC于点N,得出△ANC∽△AME,进而求出EM的长,进而得出答案.
解答 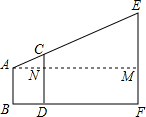 解:过点A作AM⊥EF,垂足为M,交DC于点N,
解:过点A作AM⊥EF,垂足为M,交DC于点N,
∵AB=180m,CD=240m,BD=30m,DF=420m,
∴CN=240-180=60(m),AN=BD=30m,DF=MN=420m,
∵DC∥EF,
∴△ANC∽△AME,
∴$\frac{AN}{AM}$=$\frac{CN}{EM}$,
即$\frac{30}{450}$=$\frac{60}{ME}$,
解得:ME=900,
故EF=ME+MF=900+180=1080(m).
故答案为:1080m.
点评 此题主要考查了相似三角形的应用,根据题意得出△ANC∽△AME是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.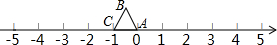 等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )
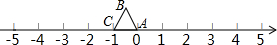 等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是( )| A. | 2013 | B. | 2010 | C. | 2011 | D. | 2012 |
6.已知线段a=l,c=5,线段b是线段a、c的比例中项,线段b的值为( )
| A. | 2.5 | B. | $\sqrt{5}$ | C. | ±2.5 | D. | ±$\sqrt{5}$ |
20.菱形ABCD的周长为16,∠A=60°,则BD的长为( )
| A. | 8 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
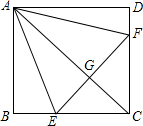 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,求证:
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,求证: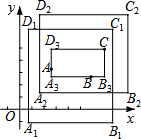 在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义: