题目内容
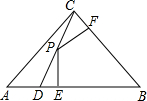 如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE⊥AB于点E,则PE+PF的值是( )
如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE⊥AB于点E,则PE+PF的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:等腰直角三角形,等腰三角形的性质
专题:
分析:据已知,过C作CH⊥AB于H,根据等腰直角三角形的性质求得CH的长度,计算△BDC的面积,再利用转化为△BPD与△BPC的面积和即可求的PE+PF的值.
解答:解:如图所示,过C作CH⊥AB于H,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,
∴CH=
,
∴S△BDC=
BD•CH=
×1×
=
,
又∵S△BCD=S△BPC+S△BPD=
BD•PE+
BC•PF=
×1×PE+
×1×PF,
∴PE+PF=
.
故答案选A.

∴CH=
| ||
| 2 |
∴S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
又∵S△BCD=S△BPC+S△BPD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PF=
| ||
| 2 |
故答案选A.

点评:此题考查的知识点是全等三角形的判定与性质及等腰三角形的性质,关键是作辅助线证矩形PGDF,再证△BPE≌△PBG.

练习册系列答案
相关题目
 如图是一个圆锥的主视图,则该圆锥的侧面积是( )
如图是一个圆锥的主视图,则该圆锥的侧面积是( )| A、6π | ||
| B、3π | ||
C、
| ||
D、
|
方程
-
=0的解是( )
| 2 |
| x-2 |
| 4x |
| x2-4 |
| A、无解 | B、x=-2 |
| C、x=2 | D、x=±2 |
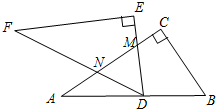 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为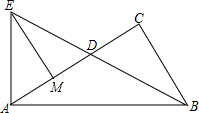 如图,在Rt△ABC中,∠C=90°,点D为AC边上一点,将线段AD绕点A逆时针旋转到线段AE,使得AE⊥AB,且点E、D、B恰好在同一直线上,作EM⊥AC于点M.
如图,在Rt△ABC中,∠C=90°,点D为AC边上一点,将线段AD绕点A逆时针旋转到线段AE,使得AE⊥AB,且点E、D、B恰好在同一直线上,作EM⊥AC于点M. 如图,在△ABC中,AD,BE,CF是三条高,交点为H,延长AH交外接圆于点M,
如图,在△ABC中,AD,BE,CF是三条高,交点为H,延长AH交外接圆于点M,