题目内容
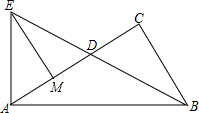 如图,在Rt△ABC中,∠C=90°,点D为AC边上一点,将线段AD绕点A逆时针旋转到线段AE,使得AE⊥AB,且点E、D、B恰好在同一直线上,作EM⊥AC于点M.
如图,在Rt△ABC中,∠C=90°,点D为AC边上一点,将线段AD绕点A逆时针旋转到线段AE,使得AE⊥AB,且点E、D、B恰好在同一直线上,作EM⊥AC于点M.(1)若线段AD逆时针旋转了54°,求∠CBD的度数;
(2)求证:AB=EM+BC.
考点:旋转的性质,全等三角形的判定与性质
专题:证明题
分析:(1)根据旋转的性质可得AD=AE,∠DAE=54°,再根据等腰三角形两底角相等求出∠ADE,根据对顶角相等可得∠BDC=∠ADE,然后利用直角三角形两锐角互余列式计算即可得解;
(2)过点D作DF⊥AB于F,根据同角的余角相等求出∠AEM=∠DAF,再利用“角角边”证明△AEM和△DAF全等,根据全等三角形对应边相等可得AF=EM,再根据等角的余角相等求出∠CBD=∠ABD,然后利用角平分线上的点到角的两边距离相等可得CD=DF,利用“HL”证明Rt△BCD和Rt△BFD全等,根据全等三角形对应边相等可得BC=BF,再根据AB=AF+BF等量代换即可得证.
(2)过点D作DF⊥AB于F,根据同角的余角相等求出∠AEM=∠DAF,再利用“角角边”证明△AEM和△DAF全等,根据全等三角形对应边相等可得AF=EM,再根据等角的余角相等求出∠CBD=∠ABD,然后利用角平分线上的点到角的两边距离相等可得CD=DF,利用“HL”证明Rt△BCD和Rt△BFD全等,根据全等三角形对应边相等可得BC=BF,再根据AB=AF+BF等量代换即可得证.
解答:(1)解:由旋转的性质得,AD=AE,∠DAE=54°,
∴∠ADE=
(180°-∠DAE)=
(180°-54°)=63°,
∵∠BDC=∠ADE=63°,∠C=90°,
∴∠CBD=90°-∠BDC=90°-63°=27°;
(2)证明:如图,过点D作DF⊥AB于F,
∵AE⊥AB,EM⊥AC,
∴∠AEM+∠EAM=∠DAF+∠EAM=90°,
∴∠AEM=∠DAF,
在△AEM和△DAF中,
,
∴△AEM≌△DAF(AAS),
∴AF=EM,
∵∠CBD+∠BDC=90°,
∠ABD+∠AED=90°,
∠AED=∠ADE=∠BDC,
∴∠CBD=∠ABD,
∴CD=DF,
在Rt△BCD和Rt△BFD中,
,
∴Rt△BCD≌Rt△BFD(HL),
∴BC=BF,
由图可知,AB=AF+BF,
∴AB=EM+BC.
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BDC=∠ADE=63°,∠C=90°,
∴∠CBD=90°-∠BDC=90°-63°=27°;
(2)证明:如图,过点D作DF⊥AB于F,
∵AE⊥AB,EM⊥AC,
∴∠AEM+∠EAM=∠DAF+∠EAM=90°,
∴∠AEM=∠DAF,
在△AEM和△DAF中,
|

∴△AEM≌△DAF(AAS),
∴AF=EM,
∵∠CBD+∠BDC=90°,
∠ABD+∠AED=90°,
∠AED=∠ADE=∠BDC,
∴∠CBD=∠ABD,
∴CD=DF,
在Rt△BCD和Rt△BFD中,
|
∴Rt△BCD≌Rt△BFD(HL),
∴BC=BF,
由图可知,AB=AF+BF,
∴AB=EM+BC.
点评:本题考查了旋转的性质,全等三角形的判定与性质,等边对等角的性质,角平分线上的点到角的两边距离相等的性质,熟记各性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
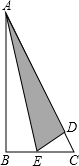 如图所示的三角形纸片中∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上,折痕为AE.则BE的长为
如图所示的三角形纸片中∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上,折痕为AE.则BE的长为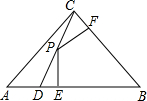 如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE⊥AB于点E,则PE+PF的值是( )
如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE⊥AB于点E,则PE+PF的值是( ) 如图,把△ABC向上平移4个单位长度,再向右平移2个单位长度得到△DEF.
如图,把△ABC向上平移4个单位长度,再向右平移2个单位长度得到△DEF.