题目内容
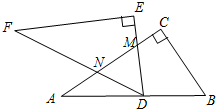 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为考点:旋转的性质
专题:
分析:作辅助线,利用相似三角形、勾股定理、等腰三角形的性质,列方程求解
解答: 解:如图所示:
解:如图所示:
过点D作DK⊥AC于点K,则DK∥BC,
又∵点D为AB中点,
∴DK=
BC=3.
∵DM=MN,∴∠MND=∠MDN,由∠MDN=∠B,
∴∠MND=∠B,又∵∠DKN=∠C=90°,
∴△DKN∽△ACB,
∴
=
,即
=
,得KN=
.
设DM=MN=x,则MK=x-
.
在Rt△DMK中,由勾股定理得:MK2+DK2=MD2,
即:(x-
)2+32=x2,解得x=
,
∴S△DMN=
MN•DK=
×
×3=
.
故答案为:
.
 解:如图所示:
解:如图所示:过点D作DK⊥AC于点K,则DK∥BC,
又∵点D为AB中点,
∴DK=
| 1 |
| 2 |
∵DM=MN,∴∠MND=∠MDN,由∠MDN=∠B,
∴∠MND=∠B,又∵∠DKN=∠C=90°,
∴△DKN∽△ACB,
∴
| KN |
| BC |
| DK |
| AC |
| KN |
| 6 |
| 3 |
| 8 |
| 9 |
| 4 |
设DM=MN=x,则MK=x-
| 9 |
| 4 |
在Rt△DMK中,由勾股定理得:MK2+DK2=MD2,
即:(x-
| 9 |
| 4 |
| 25 |
| 8 |
∴S△DMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 8 |
| 75 |
| 16 |
故答案为:
| 75 |
| 16 |
点评:此题主要考查了旋转的性质以及相似三角形的性质和勾股定理等知识,得出(x-
)2+32=x2是解题关键.
| 9 |
| 4 |

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
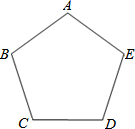 如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下: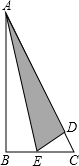 如图所示的三角形纸片中∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上,折痕为AE.则BE的长为
如图所示的三角形纸片中∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上,折痕为AE.则BE的长为 如图,AB∥CD,∠ABE=60°,∠F=50°,则∠E的度数为
如图,AB∥CD,∠ABE=60°,∠F=50°,则∠E的度数为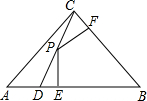 如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE⊥AB于点E,则PE+PF的值是( )
如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE⊥AB于点E,则PE+PF的值是( )