题目内容
现有A、B、C、D四张卡片，上面分别写有2，π，
，
，四个实数，先随机的摸出一张卡片不放回，再随机的摸出一张卡片，则两次摸到的卡片上都是无理数的概率是 ．
| 3 |
| 3 |
| 7 |
考点：列表法与树状图法
专题：计算题
分析：列表得出所有等可能的情况数，找出两次摸到的卡片上都是无理数的情况数，即可求出所求的概率．
解答：解：列表得：（其中有理数为2，
；无理数为π，
）
所有等可能的情况有12种，其中两次摸到的卡片上都是无理数的情况有2种，
则P=
=
．
故答案为：
| 3 |
| 7 |
| 3 |
| 有 | 无 | 无 | 有 | |
| 有 | --- | （无，有） | （无，有） | （有，有） |
| 无 | （有，无） | --- | （无，无） | （有，无） |
| 无 | （有，无） | （无，无） | --- | （有，无） |
| 有 | （有，有） | （无，有） | （无，有） | --- |
则P=
| 2 |
| 12 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
如图，甲、乙两人想在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，其作法如下：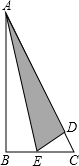
如图所示的三角形纸片中∠B=90°，AC=13，BC=5．现将纸片进行折叠，使得顶点B落在AC边上，折痕为AE．则BE的长为
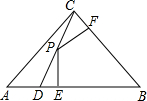如图，D是Rt△ABC斜边AB上一点，且BD=BC=AC=1，P为CD上任意一点，PF⊥BC于点F，PE⊥AB于点E，则PE+PF的值是（ ）