题目内容
14.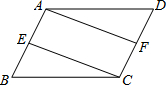 如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.
如图,在?ABCD中,E,F分别是AB,CD的中点,连接AF,CE.(1)求证:△ADF≌△CBE;
(2)连接AC,若AC=BC,判断四边形AECF是什么特殊四边形,并证明你的结论.
分析 (1)直接利用平行四边形的性质得出AB=DC,BC=AD,∠B=∠D,进而利用全等三角形的判定与性质得出答案;
(2)利用平行四边形的判定得出四边形AECF是平行四边形,进而利用矩形的判定方法得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,BC=AD,∠B=∠D,
∵E,F分别是AB,CD的中点,
∴BE=FC,
在△ADF和△CBE中
$\left\{\begin{array}{l}{FC=BE}\\{∠D=∠B}\\{AD=BC}\end{array}\right.$,
∴△ADF≌△CBE(SAS);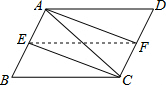
(2)解:四边形AECF是矩形,
理由:如图所示:连接EF,
∵AE=CF,且AE∥CF,
∴四边形AECF是平行四边形,
又∵AC=BC=EF,
∴四边形AECF是矩形.
点评 此题主要考查了平行四边形的判定与性质以及矩形的判定等知识,正确掌握平行四边形的判定与性质是解题关键.

练习册系列答案
相关题目
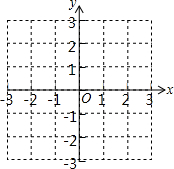 我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|.
我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|. 先阅读材料,解答下列问题:
先阅读材料,解答下列问题: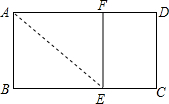 如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=$\frac{\sqrt{5}+1}{2}$.
如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=$\frac{\sqrt{5}+1}{2}$.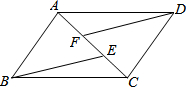 如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.
如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.