题目内容
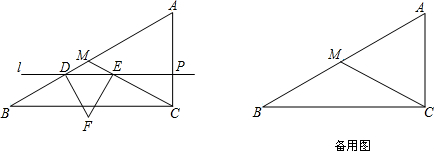
19.如图,Rt△ABC中,M为斜边AB上一点,且MB=MC=AC=8cm,平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移,运动到经过点M时停止.直线l分别交线段MB、MC、AC于点D、E、P,以DE为边向下作等边△DEF,设△DEF与△MBC重叠部分的面积为S(cm2),直线l的运动时间为t(秒).(1)求边BC的长度;
(2)求S与t的函数关系式;
(3)在整个运动过程中,是否存在这样的时刻t,使得以P、C、F为顶点的三角形为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
(4)在整个运动过程中,是否存在这样的时刻t,使得以点D为圆心、BD为半径的圆与直线EF相切?若存在,请求出t的值;若不存在,请说明理由.
分析 (1)利用直角三角形的性质和锐角三角函数即可,
(2)分两段求出函数关系式:当0<t≤3时,S=-$\frac{7\sqrt{3}}{3}$t2+8$\sqrt{3}$t,当3<t≤4时,S=3$\sqrt{3}$t2-24$\sqrt{3}$t+48$\sqrt{3}$
(3)当0<t≤3时,∠FCP≥90°,故△PCF不可能为等腰三角形当3<t≤4时,若△PCF为等腰三角形,也只能FC=FP,$\frac{t}{2}$=3(4-t),得t=$\frac{24}{7}$.
(4)若相切,利用点到圆心的距离等于半径列出方程即可.
解答 解:(1)设∠B=α,
∵MB=MC,
∴∠B=MCB=α,
∴∠AMC=2α,
∵MC=MA,
∴∠A=∠AMC=2α,
∵∠B+∠A=90°,
∴α+2α=90°,
∴α=30°,
∴∠B=30°,
∵cotB=$\frac{BC}{AC}$,
∴BC=AC×cotB=8$\sqrt{3}$;
(2)由题意,若点F恰好落在BC上,
∴MF=4(4-t)=4,
∴t=3.
当0<t≤3时,如图,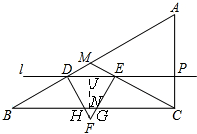
∴BD=2t,DM=8-2t,
∵l∥BC,
∴$\frac{DE}{BC}=\frac{DM}{BM}$,
∴$\frac{DE}{8\sqrt{3}}=\frac{8-2t}{8}$,
∴DE=$\sqrt{3}$(8-2t).
∴点D到EF的距离为FJ=$\frac{\sqrt{3}}{2}$DE=3(4-t),
∵l∥BC,
∴$\frac{HG}{DE}=\frac{FN}{FJ}$,
∵FN=FJ-JN=3(4-t)-t=12-4t,
∴HG=$\frac{8\sqrt{3}}{3}$(3-t)
S=S梯形DHGE=$\frac{1}{2}$(HG+DE)×FN=-$\frac{7\sqrt{3}}{3}$t2+8$\sqrt{3}$t
当3<t≤4时,重叠部分就是△DEF,
S=S△DEF=$\frac{\sqrt{3}}{4}$DE2=3$\sqrt{3}$t2-24$\sqrt{3}$t+48$\sqrt{3}$.
即:S=$\left\{\begin{array}{l}{-\frac{7\sqrt{3}}{3}{t}^{2}+8\sqrt{3}t(0<t≤3)}\\{3\sqrt{3}{t}^{2}-24\sqrt{3}t+48\sqrt{3}(3<t≤4)}\end{array}\right.$
(3)当0<t≤3时,∠FCP≥90°,
∴FC>CP,
∴△PCF不可能为等腰三角形
当3<t≤4时,若△PCF为等腰三角形,
∴只能FC=FP,
∴$\frac{t}{2}$=3(4-t),
∴t=$\frac{24}{7}$
∴存在这样的时刻t=$\frac{24}{7}$时,使得以P、C、F为顶点的三角形为等腰三角形,
(4)若相切,
理由:∵∠B=30°,
∴BD=2t,DM=8-2t,
∵l∥BC,
∴$\frac{DE}{BC}=\frac{DM}{BM}$,
∴$\frac{DE}{8\sqrt{3}}=\frac{8-2t}{8}$,
∴DE=$\sqrt{3}$(8-2t).
∴点D到EF的距离为$\frac{\sqrt{3}}{2}$DE=3(4-t)
∴2t=3(4-t),
解得t=$\frac{12}{5}$.
∴存在这样的时刻t=$\frac{12}{5}$时,使得以点D为圆心、BD为半径的圆与直线EF相切.
点评 此题是几何变换综合题,主要考查了直角三角形的性质,锐角三角函数,等腰三角形的性质,圆的切线的性质,解本题的关键利用三角函数求出线段.

 学业测评一课一测系列答案
学业测评一课一测系列答案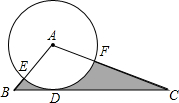 如图,在△ABC中,BC=5,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )
如图,在△ABC中,BC=5,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )| A. | 5-$\frac{8}{9}π$ | B. | 10-$\frac{8}{9}$π | C. | $\frac{8}{9}$π | D. | 5 |
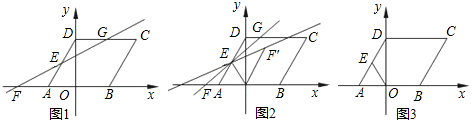

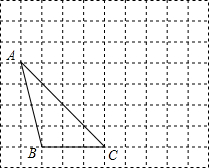 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.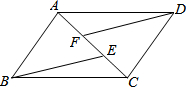 如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.
如图,在?ABCD中,点E、F在AC上,且AF=CE,求证:∠ABE=∠CDF.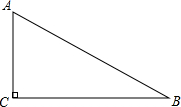 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.