题目内容
17.计算(1)5$\sqrt{27}$×$\frac{3}{2}$$\sqrt{2\frac{2}{3}}$
(2)10a2$\sqrt{ab}$×5$\sqrt{\frac{b}{a}}$÷15$\sqrt{\frac{a}{b}}$
(3)$\frac{2}{3}\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$
(4)$\frac{{2\sqrt{3}}}{{2\sqrt{3}-3}}$+$\frac{{\sqrt{3}}}{{\sqrt{3}-2}}$
(5)(5+$\sqrt{6}$)(5$\sqrt{2}$-2$\sqrt{3}$)
(6)$\frac{{a+\sqrt{ab}}}{{\sqrt{ab}+b}}$+$\frac{{\sqrt{ab}-b}}{{a-\sqrt{ab}}}$.
分析 (1)先进行二次根式的化简,然后进行乘法运算;
(2)根据二次根式的乘法发展和除法法则求解;
(3)先进行二次根式的化简,然后合并;
(4)先进行二次根式的化简,然后合并;
(5)根据二次根式的乘法法则求解;
(6)先进行二次根式的化简,然后合并.
解答 解:(1)原式=15$\sqrt{3}$×$\sqrt{6}$
=45$\sqrt{2}$;
(2)原式=50a2b÷15$\sqrt{\frac{a}{b}}$
=$\frac{10}{3}$a2$\sqrt{ab}$;
(3)原式=2$\sqrt{x}$+3$\sqrt{x}$-2$\sqrt{x}$
=3$\sqrt{x}$;
(4)原式=$\frac{2\sqrt{3}(2\sqrt{3}+3)}{3}$-3-2$\sqrt{3}$
=4+2$\sqrt{3}$-3-2$\sqrt{3}$
=1;
(5)原式=25$\sqrt{2}$-10$\sqrt{3}$+10$\sqrt{3}$-6$\sqrt{2}$
=19$\sqrt{2}$;
(6)原式=$\frac{ab+(a-b)\sqrt{ab}-ab}{b(a-b)}$+$\frac{ab+(a-b)\sqrt{ab}-ab}{a(a-b)}$
=$\frac{\sqrt{ab}}{b}$+$\frac{\sqrt{ab}}{a}$
=$\frac{\sqrt{ab}(b-a)}{ab}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及二次根式的合并.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
6.将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
| A. | 2、3、4 | B. | 4、5、6 | C. | 5、11、12 | D. | 8、15、17 |
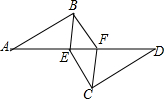 如图,AB∥CD,AB=CD,AE=DF.写出图中全等的三角形△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.
如图,AB∥CD,AB=CD,AE=DF.写出图中全等的三角形△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.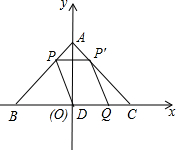 在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.
在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.