题目内容
8.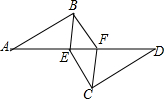 如图,AB∥CD,AB=CD,AE=DF.写出图中全等的三角形△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.
如图,AB∥CD,AB=CD,AE=DF.写出图中全等的三角形△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.
分析 利用已知结合全等三角形的判定方法分别判断得出答案.
解答 解:∵AB∥CD,
∴∠A=∠D,
∵AE=DF,
∴AF=DE,
在△ABF和△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠A=∠D}\\{AF=ED}\end{array}\right.$,
∴△ABF≌△DCE(SAS),
在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠D}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∵△ABF≌△DCE,
∴∠BFE=∠FEC,BF=EC,
在△BEF和△CFE中,
$\left\{\begin{array}{l}{BF=EC}\\{∠BFE=∠CEF}\\{EF=EF}\end{array}\right.$,
∴△BEF≌△CFE(SAS).
故答案为:△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.
点评 此题主要考查了全等三角形的判定与性质,正确利用SAS得出全等三角形是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.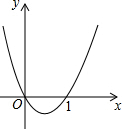 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )| A. | ①④ | B. | ②③④ | C. | ③④⑤ | D. | ①③⑤ |
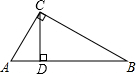 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=2$\sqrt{6}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=3,BD=8,则CD=2$\sqrt{6}$. 已知抛物线y=x2-2x-3.
已知抛物线y=x2-2x-3.