题目内容
8.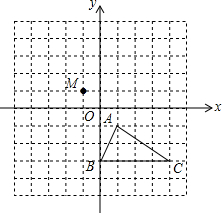 在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).(1)画出△ABC向左平移2个单位,然后再向上平移4个单位后的△A1B1C1;
(2)画出△A1B1C1绕点M(-1,1)旋转180°后得到的△A2B2C2,则以A1,C2,A2,C1为顶点的四边形的面积为12.
分析 (1)利用网格特点和平移的性质画出点A、B、C的对应点A1、B1、C1,则可得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A1、B1、C1对应点A2、B2,C2,则可得到△A2B2C2;然后利用菱形的面积公式计算以A1,C2,A2,C1为顶点的四边形的面积.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2,为所作;以A1,C2,A2,C1为顶点的四边形的面积=$\frac{1}{2}$×4×6=12.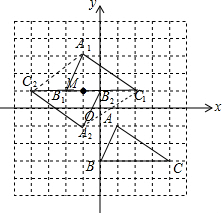
故答案为12.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
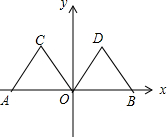 如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.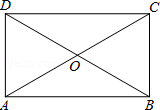 如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.
如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.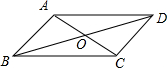 已知?ABCD,边AB=4,AD=8;对角线AC=6,BD=10,则OA=3,BD=5,周长=24.
已知?ABCD,边AB=4,AD=8;对角线AC=6,BD=10,则OA=3,BD=5,周长=24.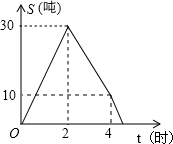 某储运部紧急调拨一批物资,连续4小时调进物资,当开始调进物资2小时后又同时开始调出物资,储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,下列说法:
某储运部紧急调拨一批物资,连续4小时调进物资,当开始调进物资2小时后又同时开始调出物资,储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,下列说法: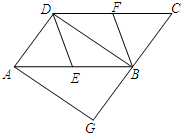 如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB,交CB的延长线于点G,∠G=90°.
如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB,交CB的延长线于点G,∠G=90°.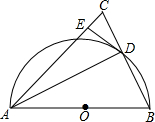 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.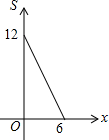
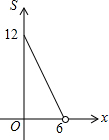
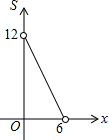

 如图,在?ABCD中,AC、BD相交于点O,AC=10,BD=8,CD=6,求△OAB的周长.
如图,在?ABCD中,AC、BD相交于点O,AC=10,BD=8,CD=6,求△OAB的周长.