题目内容
3.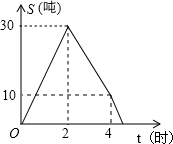 某储运部紧急调拨一批物资,连续4小时调进物资,当开始调进物资2小时后又同时开始调出物资,储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,下列说法:
某储运部紧急调拨一批物资,连续4小时调进物资,当开始调进物资2小时后又同时开始调出物资,储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,下列说法:①调进物资的速度为15吨/小时;
②调出物资的速度为25吨/小时;
③当调进物资4小时的时候,储运部库存物资为10吨;
④这批物资从开始调进到全部调出需要的时间是4.4小时.
其中正确的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据函数图象可知,前2小时调进物资30吨,可以计算出调进物资的速度,调进物资共用4小时,且速度保持不变,则4小时的时候已经调进结束,且共调进物资60吨,在2个小时内调出物资50吨,可计算出调出物资的速度以及用时.
解答 解:①由图可得,2小时调进物资30吨,调进物资的速度为15吨/小时,故①正确;
②由图可得,4小时共调进物资60吨,调出物资2个小时后仓库还剩10吨,说明调出速度为(60-10)÷2=25吨/小时,故②正确;
③由图可得,当t=4时,S=10,即调进物资4小时的时候,储运部库存物资为10吨,故③正确;
④由图可得,60吨物资全部调出需要的时间为:60÷25=2.4(时),这批物资从开始调进到全部调出需要的时间是2+2.4=4.4小时,故④正确.
故选(A)
点评 本题以实际问题为背景考查了一次函数的应用,关键是根据调运的物资除以调运的时间,求得调运的速度,考查了学生的推理能力.解题时需注意调进物资共4小时,而2小时后调进物资和调出物资同时进行.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.一个正方形的面积为2,则它的边长是( )
| A. | 4 | B. | ±$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
18.∠α的余角为65°,则∠α的度数为( )
| A. | 35° | B. | 25° | C. | 45° | D. | 65° |
15.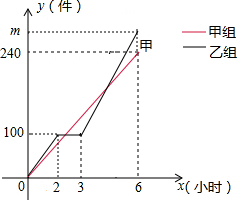 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )| A. | 甲组加工零件数量y与时间x的关系式为y甲=40x | |
| B. | 乙组加工零件总量m=280 | |
| C. | 经过2$\frac{1}{2}$小时恰好装满第1箱 | |
| D. | 经过4$\frac{3}{4}$小时恰好装满第2箱 |
13.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
| A. | 1:2:3:4 | B. | 2:2:3:3 | C. | 2;3:2:3 | D. | 2:3:3:2 |
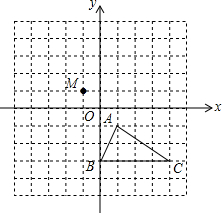 在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).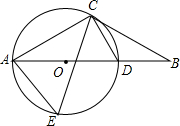 如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.
如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.