题目内容
17.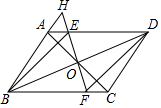 如图,在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线FH分别交AD、BC于点E、F,交BA延长线于点H,且EF⊥BD,连接BE、DF.
如图,在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线FH分别交AD、BC于点E、F,交BA延长线于点H,且EF⊥BD,连接BE、DF.(1)求证:四边形BEDF是菱形;
(2)若AC⊥AB,AB=3,BC=5,求AE的长.
分析 (1)由平行四边形的性质得出AD∥BC,OB=OD,OA=OC,AD=BC,由ASA证明△ODE≌△OBF,得出DE=BF,证出四边形BEDF是平行四边形,即可得出结论;
(2)由勾股定理求出AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4,得出OA=$\frac{1}{2}$AC=2,证明△ABO∽△AOH,得出对应边成比例求出AH=$\frac{4}{3}$,求出BH=AB+AH=$\frac{13}{3}$,再证明△AEH∽△BFH,得出$\frac{AE}{BF}=\frac{AH}{BH}$=$\frac{4}{13}$,即可得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,OA=OC,AD=BC,
∴∠ODE=∠OBF,
在△ODE和△OBF中,$\left\{\begin{array}{l}{∠ODE=∠OBF}&{\;}\\{OD=OB}&{\;}\\{∠DOE=∠BOF}&{\;}\end{array}\right.$,
∴△ODE≌△OBF(ASA),
∴DE=BF,
又∵AD∥BC,
∴四边形BEDF是平行四边形,
又∵EF⊥BD,
∴四边形BEDF是菱形;
(2)解:∵DE=BF,AD=BC,
∴AE=CF,
∵AC⊥AB,AB=3,BC=5,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4,
∴OA=$\frac{1}{2}$AC=2,
∵AC⊥AB,EF⊥BD,
∴∠BAO=∠HAO=90°,∠ABO+∠AOB=90°,∠AOH+∠AOB=90°,
∴∠ABO=∠AOH,
∴△ABO∽△AOH,
∴$\frac{OA}{AH}=\frac{AB}{OA}$,即$\frac{2}{AH}=\frac{3}{2}$,
解得:AH=$\frac{4}{3}$,
∴BH=AB+AH=$\frac{13}{3}$,
∵AD∥BC,
∴△AEH∽△BFH,
∴$\frac{AE}{BF}=\frac{AH}{BH}$=$\frac{4}{13}$,
即$\frac{AE}{5-AE}=\frac{4}{13}$,
解得:AE=$\frac{20}{17}$.
点评 本题考查了菱形的判定、平行四边形的判定、全等三角形的判定与性质、勾股定理、相似三角形的判定与性质等知识;本题综合性强,有一定难度.

 某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )
某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )| A. | 第一天 | B. | 第二天 | C. | 第三天 | D. | 第四天 |
| A. | 了解中央电视台新闻频道的收视率应采用全面调查 | |
| B. | 了解岳池县初一年级学生的视力情况,现在我县城区甲、乙两所中学的初一年级随机地各抽取50名学生的视力情况 | |
| C. | 反映岳池县6月份每天的最高气温的变化情况适合用折线统计图 | |
| D. | 商家从一批粽子中抽取200个进行质量检测,200是总体 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
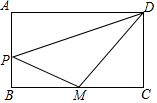 如图.长方形ABCD长为10厘米,宽为6厘米,M为BC的中点,三角形PMD面积为25平方厘米.那么三角形APD的面积为多少平方厘米?
如图.长方形ABCD长为10厘米,宽为6厘米,M为BC的中点,三角形PMD面积为25平方厘米.那么三角形APD的面积为多少平方厘米?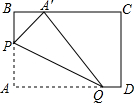 在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.
在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.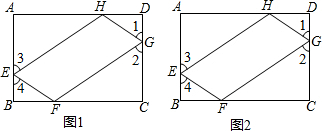
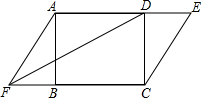 如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.
如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.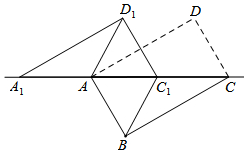 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论: