题目内容
2.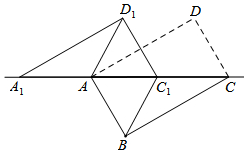 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论:①△A1AD1≌△CC1B;
②当x=1时,△BDD1为直角三角形;
③在平移过程中,四边形ABC1D1始终是平行四边形;
④S=$\frac{\sqrt{3}}{4}$(x-2)2(0<x<2);
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由矩形的性质及平移的性质易得∠A1=∠DAC,A1D1=AD,AA1=CC1,结论显然;②由所给条件可证明△AC1B是等边三角形,ABC1D1自然是菱形;易得△AC1F∽△ACD,根据面积比等于相似比平方可得出s与x的函数关系式.
解答 解:∵四边形ABCD为矩形,
∴BC=AD,BC∥AD,
∴∠DAC=∠ACB,
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,$\left\{\begin{array}{l}{A{A}_{1}=C{C}_{1}}\\{∠{A}_{1}=∠ACB}\\{{A}_{1}{D}_{1}=CB}\end{array}\right.$
∴△A1AD≌△CC1B,故①正确.
②∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,
∴△AC1B是等边三角形,
∴AB=D1C1,
又AB∥BC1,
∴四边形ABC1D1是菱形,
∴BD1⊥AC1.
又∵DD1∥AC1,
∴BD1⊥DD1.
∴△BDD1为直角三角形,故②正确.
∵四边形ABC1D1是菱形,
∴四边形ABC1D1是平行四边形,故③正确.
如图所示:
∵C1D1∥CD,
∴△AC1F∽△ACD,
∴$\frac{{S}_{△A{C}_{1}F}}{{S}_{△ACD}}$=($\frac{2-x}{2}$)2,
∴S=$\frac{1}{2}$DC•AD•($\frac{2-x}{2}$)2=$\frac{1}{2}$×1×$\sqrt{3}$•($\frac{2-x}{2}$)2=$\frac{\sqrt{3}}{8}$(2-x)2.故④错误.
故选:C.
点评 本题考查了矩形的性质、平移变换、全等三角形的判定与性质、等边三角形的判定与性质、菱形的判定、相似三角形的判定与性质等知识点,综合性较强,难度中等.清楚矩形、菱形等基本几何图形的性质以及平移变换的特征是解决本题的关键.

| A. | 四个角都是直角 | B. | 四条边相等 | C. | 对角线相等 | D. | 对角线互相平分 |
| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
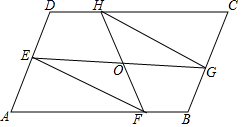 如图所示,在平行四边形ABCD中,点E、F、G、H分别在AD、AB、BC、CD上.且DE=BG,AF=CH,求证:(1)EF=GH;(2)EG和HF互相平分.
如图所示,在平行四边形ABCD中,点E、F、G、H分别在AD、AB、BC、CD上.且DE=BG,AF=CH,求证:(1)EF=GH;(2)EG和HF互相平分.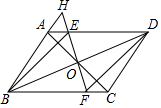 如图,在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线FH分别交AD、BC于点E、F,交BA延长线于点H,且EF⊥BD,连接BE、DF.
如图,在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线FH分别交AD、BC于点E、F,交BA延长线于点H,且EF⊥BD,连接BE、DF.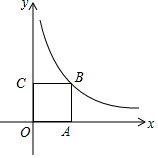 如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.
如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.