题目内容
12.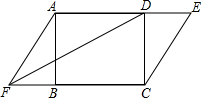 如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.
如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.(1)求证:四边形AECF是平行四边形;
(2)若DE=3,CD=4,AD=5,求证:DF平分∠AFC.
分析 (1)依据矩形的性质可知AD∥BC,且AD=BC,然后再证明AE=FC即可;
(2)依据勾股定理可求得CE=5,由矩形的性质可求得AF的长,于是得到AF=AD,然后依据等腰三角形的性质和平分线的性质进行证明即可.
解答 证明:(1)∵ABCD为矩形,
∴AD∥BC,AD=BC.
∵DE=BF,
∴AD+DE=BC+FB,即AE=FC.
又∵AE∥FC,
∴四边形AECF是平行四边形.
(2)∵ABCD为矩形,
∴∠CDE=90°.
∴CE=$\sqrt{D{C}^{2}+D{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵四边形AECF是平行四边形,
∴AF=CE=5.
又∵AD=5,
∴AD=AF.
∴∠AFD=∠ADF.
∵AD∥FC,
∴∠ADF=∠DFC.
∴∠AFD=∠DFC.
∴FD平分∠AFC.
点评 本题主要考查的是矩形的性质、平行四边形的判定、勾股定理的应用,熟练掌握相关性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
1.已知?ABCD中,∠B+∠D=200°,则∠A的度数为( )
| A. | 100° | B. | 160° | C. | 80° | D. | 60° |
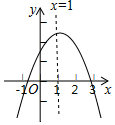 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.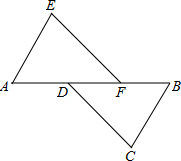 如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.
如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.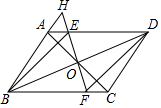 如图,在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线FH分别交AD、BC于点E、F,交BA延长线于点H,且EF⊥BD,连接BE、DF.
如图,在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线FH分别交AD、BC于点E、F,交BA延长线于点H,且EF⊥BD,连接BE、DF.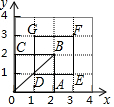 如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移$\frac{1}{2}$OB个单位,则点C的对应点坐标为(1,3).
如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移$\frac{1}{2}$OB个单位,则点C的对应点坐标为(1,3).