题目内容
8．
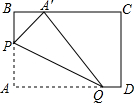在矩形纸片中，AB=3，AD=5，如图所示．折叠纸片，使点A落在BC边上的点A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P，Q也随之移动．若限定点P，Q分别在AB，AD边上移动，则移动过程中线段BA′的长度取值范围是1≤BA'≤3．
分析 根据翻折变换，当点Q与点D重合时，点A′到达最左边；当点P与点B重合时，点A′到达最右边，所以点A′就在这两个点之间移动，分别求出这两个位置时A′B的长度，即可得到线段BA′的长度取值范围．
解答 
解：如图1，当点D与点Q重合时，根据翻折对称性可得，A′D=AD=5，
在Rt△A′CD中，A′D2=A′C2+CD2，
即52=（5-A′B）2+32，
解得A′B=1，
如图2，当点P与点B重合时，根据翻折对称性可得，A′B=AB=3，
∴线段BA′的长度取值范围是：1≤BA'≤3．
故答案为：1≤BA'≤3．
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理的运用；熟练掌握矩形和翻折变换的性质，求出A′B最小和最大值是解决问题的关键．
练习册系列答案
相关题目
18．
如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D'、C'的位置．若∠CFC′=150°，则∠AED′等于（ ）
如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D'、C'的位置．若∠CFC′=150°，则∠AED′等于（ ）| A． | 50° | B． | 45° | C． | 40° | D． | 30° |
19．
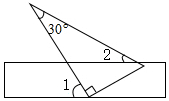如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．若∠1=55°，则图中∠2的大小为（ ）
如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．若∠1=55°，则图中∠2的大小为（ ）| A． | 25° | B． | 30° | C． | 35° | D． | 15° |
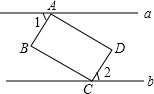如图，矩形ABCD的顶点A、C分别在直线a、b上，且a与b平行，∠2=58°，则∠1的度数为58°．
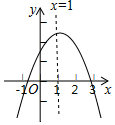如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的交点（x1，0），（x2，0），且-1＜x1＜0＜x2，有下列5个结论：①abc＜0；②b＞a+c；③a+b＞k（ka+b）（k为常数，且k≠1）；④2c＜3b；⑤若抛物线顶点坐标为（1，n），则b2=4a（c-n），其中正确的结论有（ ）个．
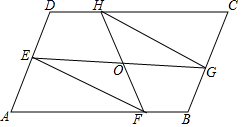如图所示，在平行四边形ABCD中，点E、F、G、H分别在AD、AB、BC、CD上．且DE=BG，AF=CH，求证：（1）EF=GH；（2）EG和HF互相平分．
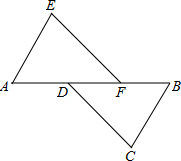如图，A，D，F，B在同一直线上，AD=BF，AE=BC，且AE∥BC．
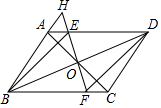如图，在平行四边形ABCD中，对角线AC与BD交于点O，过点O的直线FH分别交AD、BC于点E、F，交BA延长线于点H，且EF⊥BD，连接BE、DF．