题目内容
在一次设计比赛中,甲、乙两位参赛选手每人得到一块体积为1立方米的可塑性原料,甲用这块原料加工成一个正方体的雕塑,乙用这块原料加工成一个球体雕塑.若规定雕塑的高度不得超过1米,且加工过程中不许有损耗,请判断甲、乙两人谁的作品符合要求,并说明理由;甲、乙两人所做的作品中哪一件表面积较大?
考点:立方根
专题:应用题
分析:设正方体的边长为xm,球体雕塑的半径为ym,根据题意可得:x3=1,
πy3=1,从而可求出x、y的值,然后将x、2y与1比较,就可确定谁的作品符合要求;然后算出正方体和球体的表面积,比较它们的大小,就可确定哪一件表面积较大.
| 4 |
| 3 |
解答:解:甲、乙作品都符合要求.
理由如下:
设正方体的边长为xm,球体雕塑的半径为ym,
根据题意可得:x3=1,
πy3=1,
解得:x=1,y=
.
∴x=1,2y=2×
<1,
∴甲、乙作品都符合要求.
∵x=1,y=
,
∴正方体的表面积为6×12=6,
球的表面积为4π×(
)2=
.
∵63=216>36π,
∴6>
,
∴甲所做的作品的表面积较大.
理由如下:
设正方体的边长为xm,球体雕塑的半径为ym,
根据题意可得:x3=1,
| 4 |
| 3 |
解得:x=1,y=
| 3 |
| ||
∴x=1,2y=2×
| 3 |
| ||
∴甲、乙作品都符合要求.
∵x=1,y=
| 3 |
| ||
∴正方体的表面积为6×12=6,
球的表面积为4π×(
| 3 |
| ||
| 3 | 36π |
∵63=216>36π,
∴6>
| 3 | 36π |
∴甲所做的作品的表面积较大.
点评:本题主要考查了正方体的体积和表面积公式、球体的体积和表面积公式,属于基本题.

练习册系列答案
相关题目
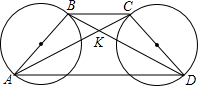 如图,梯形ABCD两对角线交于点K,分别以AB、CD为直径各作一圆,K位于两圆之外.证明:由点K向这两个圆所作的切线长相等.
如图,梯形ABCD两对角线交于点K,分别以AB、CD为直径各作一圆,K位于两圆之外.证明:由点K向这两个圆所作的切线长相等.