题目内容
13. 在下面过程中的横线上填空,并在括号内注明理由.
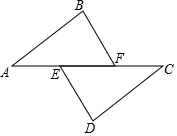
在下面过程中的横线上填空,并在括号内注明理由.已知:如图BF∥DE,BF=DE,AE=CF,说明AB与CD相等.
解:∵BF∥DE(已知)
∴∠AFB=∠CED(两直线平行,内错角相等)
∵AE=CF
∴AE+EF=CF+EF
∴AF=CE
在△ABF和△CDE中
∵AF=CE
∠AFB=∠CED
BF=DE
∴△ABF≌△CDE(SAS)
∴AB=CD(全等三角形对应边相等)
分析 首先依据平行线的性质得到∠AFB=∠CED,然后依据SAS可证明△ABF≌△CDE,最后依据全等三角形的性质可得到问题的答案.
解答 解:∵BF∥DE(已知)
∴∠AFB=∠CED(两直线平行,内错角相等)
∵AE=CF
∴AE+EF=CF+EF
∴AF=CE
在△ABF和△CDE中
∵$\left\{\begin{array}{l}{AF=CE}\\{∠AFB=∠CED}\\{BF=DE}\end{array}\right.$
∴△ABF≌△CDE(SAS)
∴AB=CD(全等三角形对应边相等).
故答案为:∠CED;两直线平行,内错角相等;AF=CE;∠AFB=∠CED;BF=DE;SAS;AB=CD;全等三角形对应边相等.
点评 本题主要考查的是全等三角形的性质和判定,熟练掌握全等三角形的性质和判定定理是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.方程3x+y=6的正整数解有( )
| A. | 1组 | B. | 2组 | C. | 4组 | D. | 无数组 |
8.把分式$\frac{2ab}{a+b}$中的a、b都扩大3倍,则分式的值( )
| A. | 扩大6倍 | B. | 不变 | C. | 扩大3倍 | D. | 缩小3倍 |
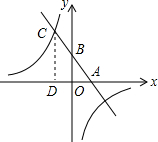 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.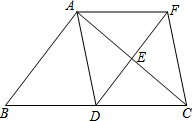 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.