��Ŀ����
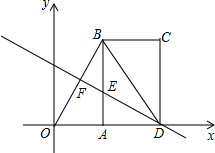 ��ͼ����ƽ��ֱ������ϵ�У���A��1��0������B��1��
��ͼ����ƽ��ֱ������ϵ�У���A��1��0������B��1��| 3 |
��1����m=
��2���ڣ�1�������������O��E��D����������ߵĽ���ʽ��
��3������FΪBO���е�ʱ����m��ֵ��
��4���ڣ�3���������£���ֱ��DF���Ƿ���ڵ�Mʹ��BDM�ǵ��������Σ������ڣ����M�����ꣻ�������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1�����ȼ����OAB�ա�EAD������ȫ�������ε��������m��ֵ��
��2�����D��E��O�������ô���ϵ������������ߵĽ���ʽ��
��3���ɵ�FΪBO���е㣬�Ƴ�DO=DB����RT��BAD�У����ù��ɶ������m��ֵ��
��4�������OF=BF�͡�BDF=��ODF=30�㣬Ȼ���3��������ۣ��ٵ�BM=BD=2ʱ���ڵ�BM=DMʱ���۵�DM=BD=2ʱ���ֱ������M�����꼴�ɣ�
��2�����D��E��O�������ô���ϵ������������ߵĽ���ʽ��
��3���ɵ�FΪBO���е㣬�Ƴ�DO=DB����RT��BAD�У����ù��ɶ������m��ֵ��
��4�������OF=BF�͡�BDF=��ODF=30�㣬Ȼ���3��������ۣ��ٵ�BM=BD=2ʱ���ڵ�BM=DMʱ���۵�DM=BD=2ʱ���ֱ������M�����꼴�ɣ�
����⣺��1������OAB�ա�EAD��
��AD=AB��
�ߵ�B��1��
����
��AB=
��
�൱m=
ʱ����OAB�ա�EAD��
�ʴ�Ϊ��
��
��2�����ɣ�1��֪��OAB�ա�EAD��
��OA=EA��
���E��������1��1��
��O��0��0����D��1+
��0����
��y=ax2+bx+c
��
��
���
��y=-
x2+
x��
��3����ͼ1��

��DF��BO��OF=BF��
��DO=DB��
��RT��BAD��BD2=AD2+AB2��
�ࣨ1+m��2=m2+��
��2��
���m=1��
��4����m=1ʱ��OD=2OA=BD=
=2��
�ߡ�OBD�ǵȱ������Σ�
��OF=BF��
���BDF=��ODF=30�㣬
�ٵ�BM=BD=2ʱ����ͼ2

�ߡ�BMD=��BDM=��ODF=30�㣬
��BM��DO��
��M��B��C���ߣ�
��M��-1��
��
����ͼ3����BM=DMʱ��

�ߡ�MBD=��MDB=30�㣬
���M���E�غϣ�
���M��1��
����
����ͼ4����DM=BD=2ʱ������M��MN��OD����ΪN��

��ND=MDcos��MDN=2��
=
��
��|MN|=MD•sin��MDN=2��
=1��
��ON=2+
��
��M��2+
��-1��
��ͼ5����DM=BD=2ʱ������M��MN��OD����ΪN��

��ND=MDcos��MDN=2��
=
��
��|MN|=MD•sin��MDN=2��
=1��
��ON=2-
��
��M��2-
��1��
��M��2-
��1����M��2+
��-1����
��AD=AB��
�ߵ�B��1��
| 3 |
��AB=
| 3 |
�൱m=
| 3 |
�ʴ�Ϊ��
| 3 |
��2�����ɣ�1��֪��OAB�ա�EAD��
��OA=EA��
���E��������1��1��
��O��0��0����D��1+
| 3 |
��y=ax2+bx+c
��
|
���
|
��y=-
| ||
| 3 |
3+
| ||
| 3 |
��3����ͼ1��

��DF��BO��OF=BF��
��DO=DB��
��RT��BAD��BD2=AD2+AB2��
�ࣨ1+m��2=m2+��
| 3 |
���m=1��
��4����m=1ʱ��OD=2OA=BD=
12+(
|
�ߡ�OBD�ǵȱ������Σ�
��OF=BF��
���BDF=��ODF=30�㣬
�ٵ�BM=BD=2ʱ����ͼ2

�ߡ�BMD=��BDM=��ODF=30�㣬
��BM��DO��
��M��B��C���ߣ�
��M��-1��
| 3 |
����ͼ3����BM=DMʱ��

�ߡ�MBD=��MDB=30�㣬
���M���E�غϣ�
���M��1��
| ||
| 3 |
����ͼ4����DM=BD=2ʱ������M��MN��OD����ΪN��

��ND=MDcos��MDN=2��
| ||
| 2 |
| 3 |
��|MN|=MD•sin��MDN=2��
| 1 |
| 2 |
��ON=2+
| 3 |
��M��2+
| 3 |
��ͼ5����DM=BD=2ʱ������M��MN��OD����ΪN��

��ND=MDcos��MDN=2��
| ||
| 2 |
| 3 |
��|MN|=MD•sin��MDN=2��
| 1 |
| 2 |
��ON=2-
| 3 |
��M��2-
| 3 |
��M��2-
| 3 |
| 3 |
������������Ҫ�����˶��κ����ۺ��⣬����Ĺؼ�����ȷ��Mʹ��BDM�ǵ��������εIJ�ͬ��������ٷֱ����M�����꣮

��ϰ��ϵ�д�
 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
�����Ŀ
���и�ʽ�У���ȷ���Ǹ����У�������
��
+2=2
����
+
=a+b����
+
=
����3
+2
=5
��
��
| 2 |
| 2 |
| a |
| ab |
| 1 | ||
|
| 2 |
| 3 |
| 2 |
| 2 |
| a |
| a |
| a |
| A��1�� | B��2�� | C��3�� | D��0�� |
 ��ͼ����ƽ��ֱ������ϵ�У���A��B�ڵ�һ���ޣ�AB��x�ᣬAB=2����Q��6��0��������ͼ��ش�
��ͼ����ƽ��ֱ������ϵ�У���A��B�ڵ�һ���ޣ�AB��x�ᣬAB=2����Q��6��0��������ͼ��ش�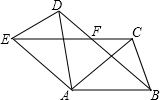 ��ͼ����ABC�У�AB=AC����BAC=40�㣬����ABC�Ƶ�A����ʱ�뷽����ת100��õ���ADE������BD��CE���ڵ�F��
��ͼ����ABC�У�AB=AC����BAC=40�㣬����ABC�Ƶ�A����ʱ�뷽����ת100��õ���ADE������BD��CE���ڵ�F�� ��ͼ����֪���κ���y=ax2+bx-
��ͼ����֪���κ���y=ax2+bx- ��ͼ��AB��DC����ABD=30�㣬��ADB=85�㣬���ADC�͡�A�ĽǶȣ�
��ͼ��AB��DC����ABD=30�㣬��ADB=85�㣬���ADC�͡�A�ĽǶȣ� ��֪��һ�κ���y=kx+b��ͼ����㣨-1��3������3��1����
��֪��һ�κ���y=kx+b��ͼ����㣨-1��3������3��1����