题目内容
 如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:
如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:(1)点B的坐标是
(2)分别求出OA,BC所在直线的解析式;
(3)P是一动点,在折线OABC上沿O→A→B→C运动,不与O、C重合,点P(x,y),△OPQ的面积为S,求S与x的函数关系式,并指出自变量x的取值范围.
考点:一次函数综合题
专题:
分析:(1)根据已知条件和平行线的性质即可求得.
(2)待定系数法即可求得.
(3)分别讨论:当P点在OA上时,当P点在AB上时,当P点在BC上时,三角形的高的情况,根据直线的解析式表示出P的坐标,即可求得.
(2)待定系数法即可求得.
(3)分别讨论:当P点在OA上时,当P点在AB上时,当P点在BC上时,三角形的高的情况,根据直线的解析式表示出P的坐标,即可求得.
解答: 解:(1)∵A(2,4),AB=2,AB∥x轴,
解:(1)∵A(2,4),AB=2,AB∥x轴,
∴B(4,4);
(2)∵A(2,4),
设直线OA为y=k1x,
∴4=2k1 解得:k1=2,
∴直线OA解析式为y=2x;
∵B(4,4),C(8,0);
设直线BC为y=k2x+b,
∴
解得
,
∴直线BC的解析式为y=-x+8;
(3)当P点在OA上时,∵直线OA为y=2x,
∴P(x,2x),
∴S=
OQ•2x=
×6×2x=6x(0<x<2);
当P点在AB上时,∵AB∥x轴,g
∴P(x,4),
∴S=
OQ×4=
×6×4=12(2≤x≤4);
当P点在BC上时,∵直线BC的解析式为y=-x+8;
∴P(x,-x+8),
∴S=
OQ•(-x+8)=
×6(-x+8)=-3x+24(4<x<8).
故S=
;
 解:(1)∵A(2,4),AB=2,AB∥x轴,
解:(1)∵A(2,4),AB=2,AB∥x轴,∴B(4,4);
(2)∵A(2,4),
设直线OA为y=k1x,
∴4=2k1 解得:k1=2,
∴直线OA解析式为y=2x;
∵B(4,4),C(8,0);
设直线BC为y=k2x+b,
∴
|
|
∴直线BC的解析式为y=-x+8;
(3)当P点在OA上时,∵直线OA为y=2x,
∴P(x,2x),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
当P点在AB上时,∵AB∥x轴,g
∴P(x,4),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
当P点在BC上时,∵直线BC的解析式为y=-x+8;
∴P(x,-x+8),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
故S=
|
点评:本题考查了平行线的性质,待定系数法求解析式以及三角形面积公式的应用等,分类讨论是本题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、两点之间直线最短 |
| B、连接两点的线段叫两点的距离 |
| C、过两点有且只有一条直线 |
| D、若点C在线段AB外,则AC+BC<AB |
 如图,在矩形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速运动到点D为止,在这个过程中,下列图象可以大致表示△APD的面积S随点P的运动时间t的变化关系的是( )
如图,在矩形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速运动到点D为止,在这个过程中,下列图象可以大致表示△APD的面积S随点P的运动时间t的变化关系的是( )




 如图,直线AB、CD相交于O,OE是∠AOD的角平分线,∠AOC=28°,求∠AOE的度数.
如图,直线AB、CD相交于O,OE是∠AOD的角平分线,∠AOC=28°,求∠AOE的度数.
 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.
如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.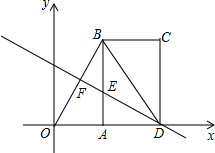 如图,在平面直角坐标系中,点A(1,0),点B(1,
如图,在平面直角坐标系中,点A(1,0),点B(1,