题目内容
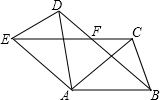 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)请直接写出四边形ABFE是哪种特殊的四边形.
考点:菱形的判定,全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)根据旋转角求出∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等.
(2)根据旋转的性质,等腰三角形的性质以及三角形内角和定理进行计算;
(3)根据对角相等的四边形是平行四边形,可证得四边形ABEF是平行四边形,然后依据邻边相等的平行四边形是菱形.
(2)根据旋转的性质,等腰三角形的性质以及三角形内角和定理进行计算;
(3)根据对角相等的四边形是平行四边形,可证得四边形ABEF是平行四边形,然后依据邻边相等的平行四边形是菱形.
解答:(1)证明:∵ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°,
又∵AB=AC,
∴AB=AC=AD=AE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS).
(2)解:∵∠CAE=100°,AC=AE,
∴∠ACE=
(180°-∠CAE)=
(180°-100°)=40°;
(3)四边形ABFE是菱形.理由如下:
解:∵∠BAD=∠CAE=140°AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=20°.
∵∠BAE=∠BAD+∠DAE=160°,
∴∠BFE=360°-∠DAE-∠ABD-∠AEC=160°,
∴∠BAE=∠BFE,
∴四边形ABEF是平行四边形,
∵AB=AE,
∴平行四边形ABEF是菱形.
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°,
又∵AB=AC,
∴AB=AC=AD=AE,
在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS).
(2)解:∵∠CAE=100°,AC=AE,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)四边形ABFE是菱形.理由如下:
解:∵∠BAD=∠CAE=140°AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=20°.
∵∠BAE=∠BAD+∠DAE=160°,
∴∠BFE=360°-∠DAE-∠ABD-∠AEC=160°,
∴∠BAE=∠BFE,
∴四边形ABEF是平行四边形,
∵AB=AE,
∴平行四边形ABEF是菱形.
点评:此题考查了全等三角形的判定与性质,等腰三角形的性质以及菱形的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列调查方式,你认为最合适的是( )
| A、了解我市每天的流动人口数,采用普查方式 |
| B、旅客上飞机前的安检,采用抽样调查 |
| C、为了了解一批炮弹的杀伤半径,采用普查方式 |
| D、为了知道某校七年级一班的数学成绩,采用普查方式 |


 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.
如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标. 已知反比例函数y=
已知反比例函数y= 如图,在平面直角坐标系中,点A(1,0),点B(1,
如图,在平面直角坐标系中,点A(1,0),点B(1, 如图,△ABC中,AB=AC,∠A=46°,DE垂直平分AB,△BEC的周长为20,BC=9.
如图,△ABC中,AB=AC,∠A=46°,DE垂直平分AB,△BEC的周长为20,BC=9. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.