题目内容
9.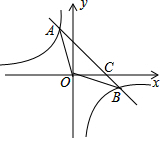 如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y=-x+2的图象与反比例函数的图象y=$\frac{k}{x}$交于A,B两点,与x轴交于点C,已知tan∠BOC=$\frac{1}{2}$.(1)求反比例函数的解析式.
(2)连接AO,求△AOB的面积.
(3)观察图象,直接写出不等式-x+2<$\frac{k}{x}$的解集.
分析 (1)设点B的坐标为(m,-m+2)(m>2),根据tan∠BOC=$\frac{1}{2}$即可得出关于m的分式方程,解之即可得出m的值,进而即可得出点B的坐标,再根据反比例函数图象上点的坐标特征即可求出反比例函数的解析式;
(2)联立两函数解析式成方程组,解之即可得出点A的坐标,再根据一次函数图象上点的坐标特征可求出点C的坐标,利用三角形的面积公式即可得出△AOB的面积;
(3)根据两函数图象的上下位置关系结合交点的横坐标,即可得出不等式的解集.
解答 解:(1)设点B的坐标为(m,-m+2)(m>2),
∵tan∠BOC=$\frac{1}{2}$,
∴-$\frac{-m+2}{m}$=$\frac{1}{2}$,
解得:m=4,
经检验,m=4是方程-$\frac{-m+2}{m}$=$\frac{1}{2}$的解,
∴点B的坐标为(4,-2),
∴k=4×(-2)=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$.
(2)联立一次函数与反比例函数解析式成方程组,
$\left\{\begin{array}{l}{y=-x+2}\\{y=-\frac{8}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=-2}\end{array}\right.$,
∴点A的坐标为(-2,4).
当y=-x+2=0时,x=2,
∴点C的坐标为(2,0),
∴S△AOB=$\frac{1}{2}$OC•(yA-yB)=$\frac{1}{2}$×2×[4-(-2)]=6.
(3)观察函数图象可知:当-2<x<0或x>4时,一次函数图象在反比例函数图象下方,
∴不等式-x+2<$\frac{k}{x}$的解集为-2<x<0或x>4.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标、解分式方程以及三角形的面积,解题的关键是:(1)解分式方程找出点B的坐标;(2)根据三角形的面积公式求出△AOB的面积;(3)根据两函数图象的上下位置关系找出不等式的解集.

| A. | $\frac{1}{x}$+x=1 | B. | 3x(x+1)=3 | C. | x3-3x=4 | D. | $\sqrt{x-1}$=5 |
| A. | |a|一定是正数 | |
| B. | 在同一平面内,过直线外或直线上一点,有且只有一条直线垂直于已知直线 | |
| C. | 两个无理数的和仍是无理数 | |
| D. | 如果两个角互补,那么一个是锐角,一个是钝角 |
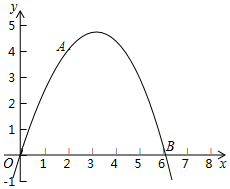 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0). 已知一次函数y=-2x-6.
已知一次函数y=-2x-6.
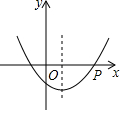 如图,抛物线y=ax2+bx+c的对称轴是经过点(1,0)且平行于y轴的直线,若点P(4,0)在抛物线上,则4a-2b+c的值为( )
如图,抛物线y=ax2+bx+c的对称轴是经过点(1,0)且平行于y轴的直线,若点P(4,0)在抛物线上,则4a-2b+c的值为( )