题目内容
18.一个矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为y=2x2-12x+28,可知当x满足条件0<x<3时.矩形的面积逐渐减小;当x满足条件x>3时,矩形的面积逐渐增大;当x=3时,矩形的面积有最小值,最小值y=10.分析 先利用配方法把二次函数解析式配成顶点式,然后根据二次函数的性质求解.
解答 解:y=2x2-12x+28
=2(x-3)2+10,
抛物线的对称轴为直线x=3,
所以当0<x<3时.矩形的面积逐渐减小;
当x>3时,矩形的面积逐渐增大;
当x=3时,矩形的面积有最小值,最小值y=10.
故答案为0<x<3,x>3,3,10.
点评 本题考查了二次函数的最值:确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
13.不等式组$\left\{\begin{array}{l}{x+1>0}\\{x-1≤0}\end{array}\right.$的解集是( )
| A. | x≥1 | B. | -1<x≤1 | C. | x<-1 | D. | 无解 |
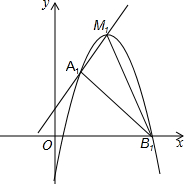 已知:抛物线Ck:y=-x2+2kx-k2+k+1(k=1,2,3…,k为正整数),抛物线Ck的顶点为Mk.
已知:抛物线Ck:y=-x2+2kx-k2+k+1(k=1,2,3…,k为正整数),抛物线Ck的顶点为Mk.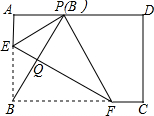 如图,在矩形ABCD中,点E、F分别在AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
如图,在矩形ABCD中,点E、F分别在AB,BC上,且AE=$\frac{1}{3}$AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )