题目内容
15.(1)因式分解:2m2n-8mn+8n.(2)解不等式组$\left\{\begin{array}{l}{x-3<1}\\{3x+2≤4}\end{array}\right.$.
分析 (1)直接提取公因式2n,进而利用完全平方公式分解因式即可;
(2)分别解不等式,进而得出不等式组的解集.
解答 解:(1)2m2n-8mn+8n
=2n(m2-4m+4)
=2n(m-2)2;
(2)$\left\{\begin{array}{l}{x-3<1①}\\{3x+2≤4②}\end{array}\right.$,
解①得:x<4,
解②得:x≤$\frac{2}{3}$,
则不等式组的解集为:x≤$\frac{2}{3}$.
点评 此题主要考查了提取公因式法以及公式法分解因式和不等式组的解法,正确掌握解题方法是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.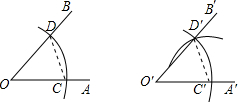 用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )
用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )
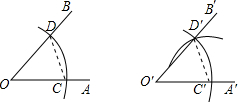 用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )
用直尺和圆规作一个角等于已知角的示意图如图,可说明△COD≌△C′O′D′,进而得出∠A′O′B′=∠AOB的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
3.小马虎在下面的计算中只做对了一道题,你认为他做对的是( )
| A. | (a+b)2=a2+b2 | B. | (2ab+b)÷b=2a | C. | -2a(b-1)=-2ab-2a | D. | (a+b)(a-b)=a2-b2 |
10. 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )
 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )| A. | 3.5 | B. | -3.5 | C. | -2.6 | D. | 2.6 |
7.下列是最简二次根式的为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{3{a}^{3}}$(a>0) |
4.下列式子没有意义的是( )
| A. | $\sqrt{0}$ | B. | $\sqrt{-5}$ | C. | $\sqrt{(-3)^{2}}$ | D. | $\sqrt{6}$ |
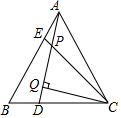 如图,△ABC是等边三角形,E,D分别是边AB,BC上的点,AE=BD,AD和CE交于点P,CQ⊥AD于点Q,若CP=8,PQ=4.
如图,△ABC是等边三角形,E,D分别是边AB,BC上的点,AE=BD,AD和CE交于点P,CQ⊥AD于点Q,若CP=8,PQ=4.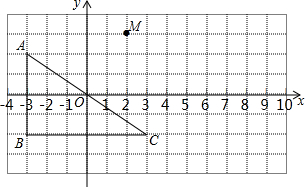 如图,已知Rt△ABC的三个顶点分别为A(-3,2),B(-3,-2),C(3,-2).将△ABC平移,使点A与点M(2,3)重合,得到△MNP.
如图,已知Rt△ABC的三个顶点分别为A(-3,2),B(-3,-2),C(3,-2).将△ABC平移,使点A与点M(2,3)重合,得到△MNP. 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题: