题目内容
5.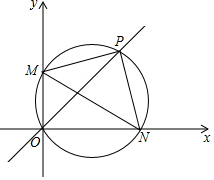 如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,
如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,(1)试判断△PMN的形状;
(2)连接MN,设直线y=x交MN于点G,若PG:PN=3:4,△PGN的周长为6,求△PON的周长.
分析 (1)首先证明出PM=PN,再证明出∠NPM=90°即可;
(2)首先证明出∠PMN=∠PNM和∠OPN=∠OPN,利用相似三角形的性质即可得到答案.
解答 (1)解:△PMN是等腰直角三角形,
理由:∵y=x,
∴∠PON=∠POM=45°.
∴PN=PM.
∵四边形ONPM内接于圆,
∴∠MON+∠NPM=180°.
∵∠MON=90°,
∴∠NPM=90°.
即△PMN是等腰直角三角形.
(2)∵△PMN是等腰直角三角形,
∴∠PMN=∠PNM
∵∠OPN=∠OPN,
∴△PNG∽△PON.
∴△PNG的周长:△PON的周长=PG:PN=3:4.
∴△PNG的周长=6,
∴△PON的周长=8.
点评 本题主要考查了圆的综合题,涉及到等腰三角形的判定与性质、园内接四边形的性质、相似三角形的判定与性质,解题的关键是证明(1)的关键是得到∠NPM=90°,证明(2)的关键是得出△PNG∽△PON.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6. 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
(1)表格中a的值为100,b的值为125.
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.| 获奖等级 | 频数 |
| 一等奖 | a |
| 二等奖 | b |
| 三等奖 | 275 |
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
3.已知$\sqrt{a-2}$+(b+$\frac{1}{2}$)2=0,则a2016b2017的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
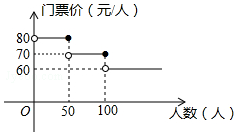 我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.