题目内容
16.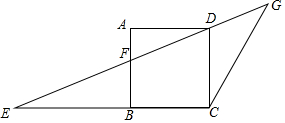 如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.
如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.(1)求证:△FAD∽△FBE;
(2)若正方形的边长为5,EF:FD:DG=2:1:1,求△ECG的面积.
分析 (1)根据正方形的性质得到∠A=∠ABC=∠ABE=90°,根据相似三角形的判定定理即可得到结论;
(2)如图,作GH⊥EC,垂足为H,得到BF∥CD∥HG,根据平行线分线段成比例定理得到$\frac{EF}{DF}=\frac{BE}{BC}$=2,得到BE=10,求得CE=15,根据相似三角形的性质得到GH=$\frac{20}{3}$,由三角形的面积公式即可得到结论.
解答 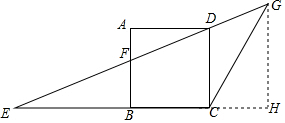 (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠ABE=90°,
∴∠FAD=∠FBE=90°,
∵∠GFB=∠DFA,
∴△FAD∽△FBE;
(2)解:如图,作GH⊥EC,垂足为H,
则BF∥CD∥HG,
∴$\frac{EF}{DF}=\frac{BE}{BC}$=2,
∴BE=10,
∴CE=15,
∵CD∥HG,
∴△CDE∽△HGE,
∴$\frac{CD}{GH}$=$\frac{DE}{EG}$,即$\frac{5}{GH}$=$\frac{3}{4}$,
∴GH=$\frac{20}{3}$,
∴△ECG的面积=$\frac{1}{2}$CE•GH=$\frac{1}{2}×$15×$\frac{20}{3}$=50.
点评 本题考查了相似三角形的判定和性质,正方形的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
7. 如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )
如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )
 如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )
如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
4.若等腰三角形中有两边长分别为3和7,则这个三角形的周长为( )
| A. | 13 | B. | 17 | C. | 10或13 | D. | 13或17 |
1.先化简:($\frac{x}{x-2}$-$\frac{4}{{x}^{2}-2x}$)÷$\frac{x+2}{{x}^{2}-x}$,然后从-2,-1,0,1,2中选取一个你喜欢的值代入求值.
6. 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
(1)表格中a的值为100,b的值为125.
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.| 获奖等级 | 频数 |
| 一等奖 | a |
| 二等奖 | b |
| 三等奖 | 275 |
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
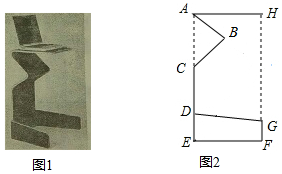 如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.
如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.