题目内容
14．若（x-p）（x-2）=x2+2p，则p的值是（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
分析 将原式左边根据多项式乘以多项式法则展开，将p看做常数合并后，结合原式右边知一次项系数为0，可得答案．
解答 解：（x-p）（x-2）=x2-2x-px+2p=x2+（-2-p）x+2p，
由题意知，-2-p=0，
解得：p=-2，
故选：A．
点评 本题主要考查多项式乘多项式，熟练掌握多项式相乘的法则，根据一次项为0得出关于p的方程是关键．
练习册系列答案
阅读快车系列答案
相关题目
4．若等腰三角形中有两边长分别为3和7，则这个三角形的周长为（ ）
| A． | 13 | B． | 17 | C． | 10或13 | D． | 13或17 |
2．
如图，直线AB∥CD，∠A=70°，∠C=40°，则∠E等于（ ）
如图，直线AB∥CD，∠A=70°，∠C=40°，则∠E等于（ ）| A． | 70° | B． | 60° | C． | 40° | D． | 30° |
9．
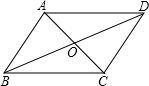如图，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形，则应增加的条件是（ ）
如图，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形，则应增加的条件是（ ）| A． | AB=CD | B． | ∠BAD=∠DCB | C． | AC=BD | D． | ∠ABC+∠BAD=180° |
6．
在某市2016年“书香校园，经典诵读”比赛活动中，有32万名学生参加比赛活动，其中有8万名学生分别获得一、二、三等奖，从获奖学生中随机抽取部分，绘制成不完整的统计表（如表），请根据图表解答下列问题．
（1）表格中a的值为100，b的值为125．
（2）扇形统计图中表示获得一等奖的扇形的圆心角为72度．
（3）估计全市有多少名学生获得三等奖？
在某市2016年“书香校园，经典诵读”比赛活动中，有32万名学生参加比赛活动，其中有8万名学生分别获得一、二、三等奖，从获奖学生中随机抽取部分，绘制成不完整的统计表（如表），请根据图表解答下列问题．| 获奖等级 | 频数 |
| 一等奖 | a |
| 二等奖 | b |
| 三等奖 | 275 |
（2）扇形统计图中表示获得一等奖的扇形的圆心角为72度．
（3）估计全市有多少名学生获得三等奖？
3．已知$\sqrt{a-2}$+（b+$\frac{1}{2}$）2=0，则a2016b2017的值是（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |