题目内容
15.(1)计算:$\frac{\sqrt{8}×\sqrt{18}}{\sqrt{2}}$-3$\sqrt{\frac{1}{2}}$(2)解方程组:$\left\{\begin{array}{l}{3x-2y=7}\\{3x-y=5}\end{array}\right.$
(3)解方程组:$\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{4}=1}\\{3x-4y-2=0}\end{array}\right.$.
分析 (1)先把各二次根式化为最简二次根式,然后进行二次根式的除法运算,再合并即可;
(2)利用加减法先求出y,然后用代入法求x;
(3)先把方程组整理得到程组整理为$\left\{\begin{array}{l}{4x-3y=12①}\\{3x-4y=2②}\end{array}\right.$,再利用①+②x-y=2③,接着利用①-③×4得y=4,然后利用代入法求x.
解答 解:(1)原式=$\frac{2\sqrt{2}×3\sqrt{2}}{\sqrt{2}}$-$\frac{3\sqrt{2}}{2}$
=6$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$
=$\frac{9\sqrt{2}}{2}$;
(2)$\left\{\begin{array}{l}{3x-2y=7①}\\{3x-y=5②}\end{array}\right.$,
①-②得-y=2,
解得y=-2,
把y=-2代入②得3x+2=5,
解得x=1,
所以方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$;
(3)方程组整理为$\left\{\begin{array}{l}{4x-3y=12①}\\{3x-4y=2②}\end{array}\right.$,
①+②得7x-7y=14,
即x-y=2③,
①-③×4得y=4,
把y=4代入③得x-4=2,
解得x=6,
所以方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程组.

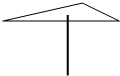 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )| A. | 三边高的交点 | B. | 三条角平分线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三边中线的交点 |
| A. | 有两条边对应相等的两个直角三角形全等 | |
| B. | 有两条边和一个叫对应相等的两个三角形全等 | |
| C. | 在同一平面内,垂直于同一直线的两条直线互相平行 | |
| D. | 三角形中至少有一个角大于60° |
| A. | (-2x3y2)3=-6x9y6 | B. | -3x2•y3=-3x6 | C. | (-x3)2=-x6 | D. | x10÷x6=x4 |
| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}≤m≤4\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |