题目内容
4.我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是( )| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}≤m≤4\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |
分析 由题目所提供的材料信息可知当菱形的“等积线段”和边垂直时最小,当“等积线段”为菱形的对角线时最大,由此可得问题答案.
解答 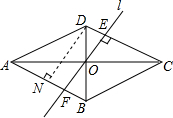 解:由“等积线段”的定义可知:当菱形的“等积线段”和边垂直时最小,
解:由“等积线段”的定义可知:当菱形的“等积线段”和边垂直时最小,
此时直线l⊥DC,过点D作DN⊥AB于点N,
则∠DAB=60°,AD=4,
故DN=AD•sin60°=2$\sqrt{3}$,
当“等积线段”为菱形的对角线时最大,
则DO=2,故AO=2$\sqrt{3}$,即AC=4$\sqrt{3}$,
则m的取值范围是:2$\sqrt{3}≤m≤4\sqrt{3}$.
故选:C.
点评 本题考查了菱形的性质以及勾股定理的运用,读懂题意,弄明白”等积线段”的定义,并准确判断出最短与最长的“等积线段”是解题的关键.

练习册系列答案
相关题目
14.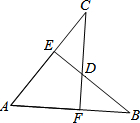 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.下列计算正确的是( )
| A. | $\sqrt{8^2}$=±8 | B. | $\frac{{\sqrt{8}}}{{\sqrt{3}}}=\frac{2}{3}\sqrt{6}$ | C. | 4$\sqrt{2}-3\sqrt{2}$=1 | D. | $\sqrt{12}×\sqrt{\frac{1}{3}}=4$ |
16.为了比较甲、乙两块地的小麦哪块长得更整齐,应选择的统计量为( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
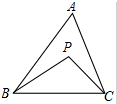 如图,在△ABC中,∠ABP=2∠PBC,∠ACP=2∠PCB.
如图,在△ABC中,∠ABP=2∠PBC,∠ACP=2∠PCB.