题目内容
已知x、y、z互不相等,x+
=y+
=z+
=k,求k的值.
| 2 |
| y |
| 2 |
| z |
| 2 |
| x |
考点:比例的性质
专题:
分析:先由x+
=k,z+
=k得出用含k、x的代数式分别表示y、z的式子,再代入y+
=k,整理得出(k2-2)x2+(2k-k3)x+2k2-4=0,由题意得出x有唯一解,即(2k-k3)2-4(k2-2)(2k2-4)=0,进而求出k的值.
| 2 |
| y |
| 2 |
| x |
| 2 |
| z |
解答:解:∵x+
=k,z+
=k,
∴y=
,z=k-
,
又∵y+
=k,
∴
+
=k,
整理得:(k2-2)x2+(2k-k3)x+2k2-4=0,
又∵x、y、z互不相等,由题可看出可互换,
∴x有唯一解,即(2k-k3)2-4(k2-2)(2k2-4)=0,
解得k2=2或8,
∴k=±
或±2
.
| 2 |
| y |
| 2 |
| x |
∴y=
| 2 |
| k-x |
| 2 |
| x |
又∵y+
| 2 |
| z |
∴
| 2 |
| k-x |
| 2 | ||
k-
|
整理得:(k2-2)x2+(2k-k3)x+2k2-4=0,
又∵x、y、z互不相等,由题可看出可互换,
∴x有唯一解,即(2k-k3)2-4(k2-2)(2k2-4)=0,
解得k2=2或8,
∴k=±
| 2 |
| 2 |
点评:本题考查了比例的性质,有一定难度.得出方程(k2-2)x2+(2k-k3)x+2k2-4=0是解题的关键.

练习册系列答案
相关题目
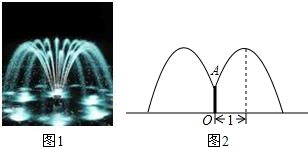 如图,天娇生态园要建造一圆形喷水池,在水池中央垂直于水面安装一个柱子OA,O恰在水面中心,OA高3米,如图1,由柱子顶端处的喷头向外喷水,水流在各方面沿形状相同的抛物线落下.
如图,天娇生态园要建造一圆形喷水池,在水池中央垂直于水面安装一个柱子OA,O恰在水面中心,OA高3米,如图1,由柱子顶端处的喷头向外喷水,水流在各方面沿形状相同的抛物线落下. 如图,长方形ABCD被分成6个小长方形,其中4个的面积已标在图中,试求未知的两个长方形的面积.
如图,长方形ABCD被分成6个小长方形,其中4个的面积已标在图中,试求未知的两个长方形的面积. 如图,在四边形ABCD中,∠B=∠D=90°,∠A=150°,AB=5,CD=15,求AD、BC的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=150°,AB=5,CD=15,求AD、BC的长.