题目内容
抛物线y=a(x-2)2的顶点A在x轴上,开口向上,与y轴相交于B点,OA=OB.
(1)求出B点的坐标;
(2)在抛物线上是否存在一点C,使△ABC是直角三角形?若存在,求出C点坐标;若不存在,请说明理由.
(1)求出B点的坐标;
(2)在抛物线上是否存在一点C,使△ABC是直角三角形?若存在,求出C点坐标;若不存在,请说明理由.
考点:二次函数的性质
专题:
分析:(1)由y=a(x-2)2,得出顶点A的坐标为(2,0),根据OA=OB,得到B(0,2);
(2)先将B(0,2)代入y=a(x-2)2,利用待定系数法求出抛物线的解析式,再分三种情况讨论:①若∠BAC=90°,则B、C关于抛物线的对称轴对称,由此求出即可;②若∠ABC=90°时,得出求出直线BC的解析式,和抛物线的解析式得出方程组,求出方程组的解即可;③若∠ACB=90°时,设C(n,k),根据勾股定理得出AC2+BC2=AB2,代入得到(n-2)2+k2+n2+(k-2)2=8,求出即可.
(2)先将B(0,2)代入y=a(x-2)2,利用待定系数法求出抛物线的解析式,再分三种情况讨论:①若∠BAC=90°,则B、C关于抛物线的对称轴对称,由此求出即可;②若∠ABC=90°时,得出求出直线BC的解析式,和抛物线的解析式得出方程组,求出方程组的解即可;③若∠ACB=90°时,设C(n,k),根据勾股定理得出AC2+BC2=AB2,代入得到(n-2)2+k2+n2+(k-2)2=8,求出即可.
解答:解:(1)∵y=a(x-2)2,
∴顶点A的坐标为(2,0),
∵抛物线y=a(x-2)2开口向上,与y轴相交于B点,OA=OB,
∴B(0,2);
(2)将B(0,2)代入y=a(x-2)2,
得2=4a,解得a=
,
∴y=
(x-2)2,即y=
x2-2x+2.
①若∠BAC=90°,
∵△AOB是等腰直角三角形,A为抛物线顶点,
∴∠BAO=45°,
∴B、C关于抛物线的对称轴对称,
∴C(4,2);
②若∠ABC=90°时,
∵直线AB的解析式为y=-x+2,AB⊥BC,
∴可设直线BC的解析式为y=x+b,
将B(0,2)代入得:b=2,
∴y=x+2,
解方程组
,
解得:
,
,
∴C(6,8);
③若∠ACB=90°时,设C(n,k),
AC2+BC2=AB2,
即(n-2)2+k2+n2+(k-2)2=8,
n2-2n+k2-2k=0,
∵k=
n2-2n+2,
代入整理得
n4-2n3+6n2-6n=0,
求出n1=0,n2=2,
∴k1=
n2-2n+2=2,k1=
n2-2n+2=0,
均不符合题意舍去.
综合上述:存在,点C的坐标是(4,2)或(6,8).
∴顶点A的坐标为(2,0),
∵抛物线y=a(x-2)2开口向上,与y轴相交于B点,OA=OB,
∴B(0,2);
(2)将B(0,2)代入y=a(x-2)2,
得2=4a,解得a=
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
①若∠BAC=90°,
∵△AOB是等腰直角三角形,A为抛物线顶点,
∴∠BAO=45°,
∴B、C关于抛物线的对称轴对称,
∴C(4,2);
②若∠ABC=90°时,
∵直线AB的解析式为y=-x+2,AB⊥BC,
∴可设直线BC的解析式为y=x+b,
将B(0,2)代入得:b=2,
∴y=x+2,
解方程组
|
解得:
|
|
∴C(6,8);
③若∠ACB=90°时,设C(n,k),
AC2+BC2=AB2,
即(n-2)2+k2+n2+(k-2)2=8,
n2-2n+k2-2k=0,
∵k=
| 1 |
| 2 |
代入整理得
| 1 |
| 4 |
求出n1=0,n2=2,
∴k1=
| 1 |
| 2 |
| 1 |
| 2 |
均不符合题意舍去.
综合上述:存在,点C的坐标是(4,2)或(6,8).
点评:本题考查了用待定系数法求出二次函数的解析式,直角三角形的性质和判定等知识点的应用,主要考查学生运用这些性质进行计算的能力,本题难度较大,对学生有较高的要求,进行分类讨论是解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,已知四边形ABCD为正方形,E,F为AB、CD的中点,AD=2,△AGF是由△ADF折叠而来的,连接GI,使得GI⊥AB.
如图,已知四边形ABCD为正方形,E,F为AB、CD的中点,AD=2,△AGF是由△ADF折叠而来的,连接GI,使得GI⊥AB. 如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为
如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为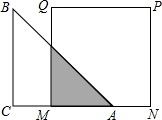 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y cm2与MA的长度x cm之间的关系式,并指出其中的常量与变量.
如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y cm2与MA的长度x cm之间的关系式,并指出其中的常量与变量.