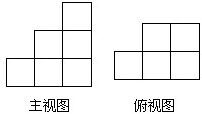
题目内容
2.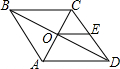 如图,已知菱形ABCD的对角线AC、BD相交于点O,AB=6cm,E是CD的中点,则OE的长为3cm.
如图,已知菱形ABCD的对角线AC、BD相交于点O,AB=6cm,E是CD的中点,则OE的长为3cm.
分析 利用菱形的对边相等以及对角线互相垂直,进而利用直角三角形斜边上的中线等于斜边的一半得出答案.
解答 解:
∵四边形ABCD是菱形,
∴AB=AD=CD=BC=6cm,
∵菱形ABCD的对角线AC、BD交于点O,
∴AC⊥BD,
∵E是CD的中点,
∴EO=$\frac{1}{2}$DC=3cm.
故答案为:3.
点评 此题主要考查了菱形的性质以及直角三角形斜边上的中线等于斜边的一半等知识,得出EO=$\frac{1}{2}$DC是解题关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
13.已知二次函数y=ax2+bx+1(a≠0)的图象的顶点在第二象限,且过点(1,0).当a-b为整数时,ab=( )
| A. | 0 | B. | $\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | -2 |
7.要证明命题“若a>b则a2>b2”是假命题,下列a,b的值能作为反例的是( )
| A. | a=-1,b=2 | B. | a=3,b=2 | C. | a=-1,b=0 | D. | a=-2,b=-1 |
14.函数y=(m-2)x+(m+1)是关于x的一次函数,那么m的取值范围是( )
| A. | m≠2 | B. | m≠-1 | C. | m=-1 | D. | m≠2且m≠-1 |
11.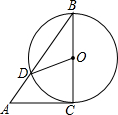 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )| A. | 100° | B. | 80° | C. | 50° | D. | 40° |
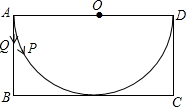 有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)
有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)