题目内容
在Rt△ABC中，∠C=90°，AC=| 36 |
| 5 |
（1）求BC的长度；
（2）分别求∠α和∠β的正弦、余弦和正切．
考点：解直角三角形
专题：
分析：（1）直接利用勾股定理得出答案；
（2）利用锐角三角函数关系分别求出即可．
（2）利用锐角三角函数关系分别求出即可．
解答：解：（1）∵∠C=90°，AC=
，AB=9，
∴BC=
=
=
；
（2）由（1）得：sinα=
=
，cosα=
=
=
，
tanα=
=
=
，sinβ═
=
=
，cosβ=
=
，
tanβ=
．
| 36 |
| 5 |
∴BC=
| AB2-AC2 |
92-(
|
| 27 |
| 5 |
（2）由（1）得：sinα=
| BC |
| AB |
| 3 |
| 5 |
| AC |
| AB |
| ||
| 9 |
| 4 |
| 5 |
tanα=
| BC |
| AC |
| ||
|
| 3 |
| 4 |
| AC |
| AB |
| ||
| 9 |
| 4 |
| 5 |
| BC |
| AB |
| 3 |
| 5 |
tanβ=
| 4 |
| 3 |
点评：此题主要考查了解直角三角形，正确选择锐角三角函数关系是解题关键．
练习册系列答案
相关题目
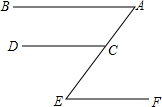如图，CD∥EF，∠ECD=∠A，则EF∥AB，说明理由如下：
如图，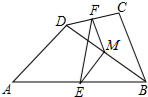
在四边形ABCD中，E、F、M分别是AB、CD、BD的中点，AD=BC．求证：∠EFM=∠FEM．反比例函数y=
（k为常数，k≠0）的自变量x的取值范围是（ ）
| k |
| x |
| A、x＞0 | B、x≠0 |
| C、x≥0 | D、k≠0 |