题目内容
用你发现的规律解答下列问题.
=1-
,
=
-
,
=
-
…
若
+
+
+…+
的值为
,求x的值.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
若
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (x+1)(x+2) |
| 2012 |
| 2013 |
考点:解分式方程
专题:规律型
分析:根据题意列出方程,利用拆项法变形,计算即可求出解.
解答:解:根据题意得:
+
+
+…+
=
,
变形得:1-
+
-
+…+
-
=
,即
=
,
解得:x=2011,
经检验x=2011是分式方程的解.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (x+1)(x+2) |
| 2012 |
| 2013 |
变形得:1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| x+1 |
| 1 |
| x+2 |
| 2012 |
| 2013 |
| x+1 |
| x+2 |
| 2012 |
| 2013 |
解得:x=2011,
经检验x=2011是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
反比例函数y=
(k为常数,k≠0)的自变量x的取值范围是( )
| k |
| x |
| A、x>0 | B、x≠0 |
| C、x≥0 | D、k≠0 |
 如图,
如图,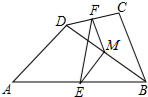 在四边形ABCD中,E、F、M分别是AB、CD、BD的中点,AD=BC.求证:∠EFM=∠FEM.
在四边形ABCD中,E、F、M分别是AB、CD、BD的中点,AD=BC.求证:∠EFM=∠FEM.