题目内容
已知△ABC中，AB=15，AC=18，∠C=30°，求S△ABC．
考点：勾股定理,含30度角的直角三角形
专题：
分析：如图，作辅助线，求出高AD，进而求出BC的长度，问题即可解决．
解答：
解：过A作AD⊥BC于D，
∵在Rt△ACD中，AC=18，∠C=30°，
∴AD=
AC=9，
由勾股定理得：
DC2=182-92，BD2=152-92，
∴DC=9
，BD=12，
∴S△ABC=
(9
+12)×9
=54+
．
解：过A作AD⊥BC于D，∵在Rt△ACD中，AC=18，∠C=30°，
∴AD=
| 1 |
| 2 |
由勾股定理得：
DC2=182-92，BD2=152-92，
∴DC=9
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
=54+
81
| ||
| 2 |
点评：该题主要考查了勾股定理及其应用问题；解题的关键是作辅助线，构造直角三角形，灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
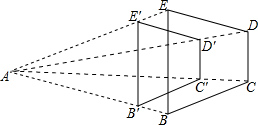如图，已知B′C′∥BC，C′D′∥CD，D′E′∥DE．
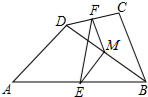在四边形ABCD中，E、F、M分别是AB、CD、BD的中点，AD=BC．求证：∠EFM=∠FEM．反比例函数y=
（k为常数，k≠0）的自变量x的取值范围是（ ）
| k |
| x |
| A、x＞0 | B、x≠0 |
| C、x≥0 | D、k≠0 |