题目内容
20．等腰梯形两底之差的一半等于它的高，那么此梯形的一个底角是（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
分析 根据已知条件和等腰梯形的性质，可推出：DF=BF，即∠D=45°，问题得解．
解答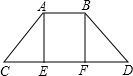 
解：如图，四边形ABCD是等腰梯形，AC=BD，AB∥CD，AE⊥CD，BF⊥CD，
∴四边形AEFB是矩形，
∴AB=EF，
∵CD-AB=CD-EF=CE+DF，CE=DF，
又∵等腰梯形两底差的一半等于它的高，
∴DF=BF，
∴∠D=45°．
故选B．
点评 本题主要考查对等腰梯形的性质，等腰三角形的性质，能把梯形转化成特殊的平行四边形和特殊三角形是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
11．一圆的半径为3，圆心到直线的距离为4，则该直线与圆的位置关系是（ ）
| A． | 相切 | B． | 相交 | C． | 相离 | D． | 以上都不对 |