题目内容
7.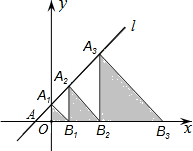 如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右第4个阴影三角形的面积是128,第2017个阴影三角形的面积是24033.
如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右第4个阴影三角形的面积是128,第2017个阴影三角形的面积是24033.
分析 根据一次函数图象上点的坐标特征结合等腰直角三角形的性质,即可得出OA1、A2B1、A3B2、A4B3的值,根据边的长度的变化即可找出变化规律“An+1Bn=BnBn+1=2n+1”,再根据三角形的面积即可得出Sn+1=$\frac{1}{2}$×(2n+1)2=22n+1,分别代入n=3、2016即可求出结论.
解答 解:当x=0时,y=x+2=2,
∴OA1=OB1=2;
当x=2时,y=x+2=4,
∴A2B1=B1B2=4;
当x=2+4=6时,y=x+2=8,
∴A3B2=B2B3=8;
当x=6+8=14时,y=x+2=16,
∴A4B3=B3B4=16.
∴An+1Bn=BnBn+1=2n+1,
∴Sn+1=$\frac{1}{2}$×(2n+1)2=22n+1.
当n=3时,S4=22×3+1=128;当n=2016时,S2017=22×2016+1=24033.
故答案为:128;
点评 本题考查了一次函数图象上点的坐标特征、等腰直角三角形以及规律型中数的变化规律,根据一次函数图象上点的坐标特征结合等腰直角三角形的性质,找出等腰直角三角形的直角边长为“An+1Bn=BnBn+1=2n+1”是解题的关键.

练习册系列答案
相关题目
17.-$\sqrt{17}$+1的小数部分是( )
| A. | -$\sqrt{17}$+5 | B. | -$\sqrt{17}$+4 | C. | -$\sqrt{17}$-3 | D. | $\sqrt{17}$-4 |
18.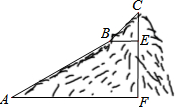 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)| A. | 500 | B. | 516 | C. | 530 | D. | 580 |
19.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
| A. | 18.1×105 | B. | 1.81×106 | C. | 1.81×107 | D. | 181×104 |
 如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=35°.
如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=35°.