题目内容
18.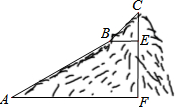 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度i=1:2,仰角∠CBE=50°,则山峰的高度CF约为( )米,(可用的参考数据:sin50°≈0.8,tan50°≈1.2,$\sqrt{5}$≈2.24)| A. | 500 | B. | 516 | C. | 530 | D. | 580 |
分析 先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
解答 解:作BH⊥AF于H,如图,
∵斜坡AB的坡度i=1:2,
∴设BH=k,AH=2k,
∴AB=$\sqrt{5}$k=800, ∴k=$\frac{800}{\sqrt{5}}$,
∴k=$\frac{800}{\sqrt{5}}$,
∴BH=$\frac{800}{\sqrt{5}}$≈356,
∴EF=BH=356m;
在Rt△CBE中,∵sin∠CBE=$\frac{CE}{BC}$,
∴CE=200•sin50°=200×0.8=160,
∴CF=CE+EF=160+356=516(m).
答:山CF的高度约为516米.
故选B.
点评 本题考查了解直角三角形的应用-坡度与坡角问题:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i═tanα.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
13.某校进行了一次数学成绩测试,甲、乙两班学生的成绩如下表所示(满分120分):
你认为哪一个班的成绩更好一些?并说明理由.
答:乙班(填“甲”或“乙”),理由是平均分甲小于乙,方差甲大于乙,乙班的成绩更好.
| 班级 | 平均分 | 众数 | 方差 |
| 甲 | 101 | 90 | 2.65 |
| 乙 | 102 | 87 | 2.38 |
答:乙班(填“甲”或“乙”),理由是平均分甲小于乙,方差甲大于乙,乙班的成绩更好.
10.下列计算正确的是( )
| A. | $\sqrt{a}$+$\sqrt{2a}$=$\sqrt{3a}$ | B. | (ab3)2=a2b5 | C. | 2a+3a=6a | D. | a•a3=a4 |

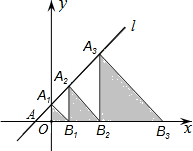 如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右第4个阴影三角形的面积是128,第2017个阴影三角形的面积是24033.
如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右第4个阴影三角形的面积是128,第2017个阴影三角形的面积是24033.