题目内容
10.已知a2+11a=-16,b2+11b=-16,求$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值.分析 由a2+11a=-16,b2+11b=-16可知a、b为方程x2+11x+16的两个根,由根与系数的关系可得出a+b=-11,ab=16,再将$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$化简成$\sqrt{\frac{(a+b)^{2}}{ab}}$,代入a+b=-11、ab=16即可得出结论.
解答 解:∵a2+11a=-16,b2+11b=-16,
∴a、b为方程x2+11x+16的两个根,
∴a+b=-11,ab=16.
$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\sqrt{(\sqrt{\frac{b}{a}}+\sqrt{\frac{a}{b}})^{2}}$=$\sqrt{\frac{b}{a}+\frac{a}{b}+2}$=$\sqrt{\frac{{a}^{2}+{b}^{2}+2ab}{ab}}$=$\sqrt{\frac{(a+b)^{2}}{ab}}$,
将a+b=-11,ab=16代入$\sqrt{\frac{(a+b)^{2}}{ab}}$中得:
$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\frac{11}{4}$
点评 本题考查了根与系数的关系以及二次根式的化简求值,解题的关键是找出a+b=-11,ab=16.本题属于基础题,难度不大,解决该题型题目时,由根与系数的关系找出两根之和与两根之积是关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
20.一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完.李永平均每天比张力多读3页.若设张力平均每天读x页,则由题意列出不等式组为( )
| A. | $\left\{\begin{array}{l}{7x>98}\\{7(x+3)>98}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7x<98}\\{7(x+3)>98}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{7x<98}\\{7x+3>98}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x>98}\\{7x+3<98}\end{array}\right.$ |
 如图,A、B、C、D是⊙O上的点,直径AB交CD于点E,已知∠C=57°,∠D=45°,则∠CEB=102°.
如图,A、B、C、D是⊙O上的点,直径AB交CD于点E,已知∠C=57°,∠D=45°,则∠CEB=102°.
 一个四边形的纸片ABCD,其中∠B=∠D=90°,把纸片按如图所示折叠,点B落在AD边上的E点,AF是折痕.
一个四边形的纸片ABCD,其中∠B=∠D=90°,把纸片按如图所示折叠,点B落在AD边上的E点,AF是折痕.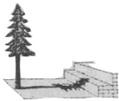 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )