题目内容
7.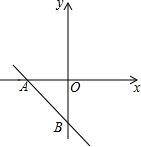 如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.
如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.(1)试证明二次函数y=x2+mx+n(m≠6)的图象与x轴有两个交点;
(2)若二次函数y=x2+mx+n图象的顶点D在直线AB上,求m,n的值;
(3)设二次函数y=x2+mx+n的图象与x轴的另一个交点为点C,顶点D关于x轴的对称点设为点E,以AE,AC为邻边作平行四边形EACF,顶点F能否在该二次函数的图象上?如果在,求出这个二次函数的表达式;如果不在,请说明理由?
分析 (1)根据待定系数法,可得n与m的关系,根据根的判别式,可得答案;
(2)根据顶点坐标公式,可得顶点坐标,根据直线上点的坐标满足函数解析式,可得关于m的方程,根据n=3m-9,可得答案;
(3)根据因式分解法,可得C点坐标,根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得E点坐标,根据平形四边顶点的坐标关系,可得F点坐标,根据F点的坐标是否满足函数解析式,可得答案.
解答 解:(1)当x=0时,y=-3,即B(0,-3),
当y=0时,-x-3=0,解得x=-3,即A点坐标(-3,0).
A(-3,0),B(0,-3),
二次函数y=x2+mx+n的图象经过点A(-3,0),则n=3m-9.
即y=x2+mx+(3m-9).
∵b2-4ac=m2-4(3m-9)=m2-12m+36=(m-6)2,
又m≠6,
∴b2-4ac>0,
则二次函数y=x2+mx+(3m-9)的图象与x轴有两个交点;
(2)二次函数y=x2+mx+n,即y=x2+mx+(3m-9).
顶点坐标为(-$\frac{m}{2}$,-$\frac{{m}^{2}}{4}$+3m-9),
因为二次函数y=x2+mx+n图象的顶点在直线AB上,
所以-$\frac{{m}^{2}}{4}$+3m-9=$\frac{m}{2}$-3,解得:m1=4,m2≠6,
则n1=3;
(3)F点不在抛物线上,理由如下:
抛物线y=x2+mx+(3m-9),
当y=0时,x2+mx+(3m-9)=0,解得x=-3,x=3-m,即C(3-m,0),A(-3,0).
顶点坐标为(-$\frac{m}{2}$,-$\frac{{m}^{2}}{4}$+3m-9),E点关于x轴的对称点是(-$\frac{m}{2}$,$\frac{{m}^{2}}{4}$-3m+9).
由EACF是平行四边形,得
xF+xA=xE+xC,yF+yA=yE+yC,
即xF=-$\frac{m}{2}$+3-m-(-3)=-$\frac{3}{2}$m+6,yF=$\frac{{m}^{2}}{4}$-3m+9+0-0=$\frac{{m}^{2}}{4}$-3m+9.
即F点坐标为(-$\frac{3}{2}$m+6,$\frac{{m}^{2}}{4}$-3m+9).
将F点的坐标代入,得
(-$\frac{3}{2}$m+6)2+m(-$\frac{3}{2}$m+6)+(3m-9)=-$\frac{3}{4}$m2+3m+27≠$\frac{{m}^{2}}{4}$-3m+9,
F点不在抛物线上.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用顶点坐标在直线上得出方程是解题关键;利用平行四边形对角顶点的关系得出F点的坐标是解题关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1134.6×108元 | B. | 11.346×1010元 | C. | 1.1346×1011元 | D. | 1.1346×1012元 |
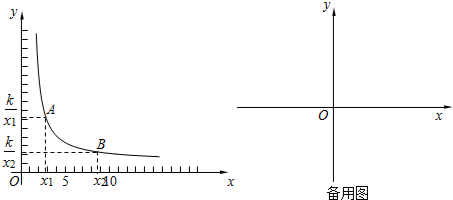
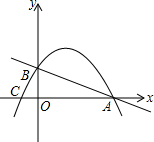 如图,已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点,过A、B两点的抛物线y=ax2+bx+c交x轴于点C(-1,0).
如图,已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点,过A、B两点的抛物线y=ax2+bx+c交x轴于点C(-1,0).



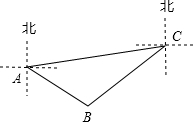 如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)