题目内容
12.已知$\frac{xy}{x+y}$=1,$\frac{yz}{y+z}$=2,$\frac{zx}{z+x}$=3,则x+y+z=-$\frac{276}{35}$.分析 已知等式变形,整理求出$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$的值,进而确定出x,y,z的值,即可求出x+y+z的值.
解答 解:由题意得:$\frac{x+y}{xy}$=1,$\frac{y+z}{yz}$=$\frac{1}{2}$,$\frac{z+x}{zx}$=$\frac{1}{3}$,即$\frac{1}{x}$+$\frac{1}{y}$=1,$\frac{1}{y}$+$\frac{1}{z}$=$\frac{1}{2}$,$\frac{1}{x}$+$\frac{1}{z}$=$\frac{1}{3}$,
∴2($\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$)=$\frac{11}{6}$,即$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=$\frac{11}{12}$,
∴$\frac{1}{x}$=$\frac{5}{12}$,$\frac{1}{y}$=$\frac{7}{12}$,$\frac{1}{z}$=-$\frac{1}{12}$,即x=$\frac{12}{5}$,y=$\frac{12}{7}$,z=-12,
则x+y+z=$\frac{12}{5}$+$\frac{12}{7}$-12=-$\frac{276}{35}$,
故答案为:-$\frac{276}{35}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.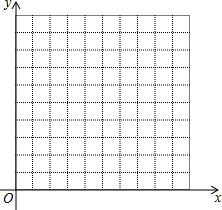 在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
(1)实验操作:
在平面直角坐标系中描出点A从点O出发,移动1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
(2)观察发现:
任一次移动,点A可能到达的点在我们学过的一种函数的图象上,
①求移动1次后点A可能到达的点所在图象的函数表达式;
②移动2次后在函数y=-2x+4的图象上,…由此我们知道,移动n次后在函数y=-2x+2n的图象上.(请填写相应的函数表达式)
(3)探索运用:
点A从点O出发经过n次移动后,到达直线y=x上的点B,且平移的总路径长为20,求点B的坐标.
 在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.
在平面直角坐标系中,点A从原点O出发,每次向上移动2个单位长度或向右移动1个单位长度.(1)实验操作:
在平面直角坐标系中描出点A从点O出发,移动1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
| A从点O出发移动次数 | 可能到达的点的坐标 |
| 1次 | (0,2),(1,0) |
| 2次 | (0,4),(1,2),(2,0) |
| 3次 | (0,6),(1,4),(2,2),(3,0) |
任一次移动,点A可能到达的点在我们学过的一种函数的图象上,
①求移动1次后点A可能到达的点所在图象的函数表达式;
②移动2次后在函数y=-2x+4的图象上,…由此我们知道,移动n次后在函数y=-2x+2n的图象上.(请填写相应的函数表达式)
(3)探索运用:
点A从点O出发经过n次移动后,到达直线y=x上的点B,且平移的总路径长为20,求点B的坐标.
6.阅读材料:在△ABC中,有一点P,当P1、A、B、C没有任何三点在同一直线上,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互补重叠的小三角形的个数情况怎样?请观察图形和表格填空.表格中的空白处应填( )

| △ABC内点的个数 | 1 | 2 | 3 | … | 12 |
| 构成不重叠的小三角形的个数 | 3 | 5 | 7 | … |

| A. | 21 | B. | 23 | C. | 25 | D. | 28 |
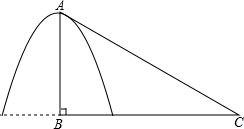 如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竿,它能否做帐篷的支撑竿,请说明理由.
如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竿,它能否做帐篷的支撑竿,请说明理由.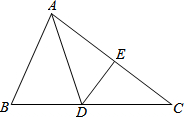 如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.
如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.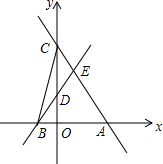 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1. 如图,⊙C经过坐标原点O,并与两坐标轴分别交于A、D两点,已知∠OBA=30°,点A的坐标为(2,O).
如图,⊙C经过坐标原点O,并与两坐标轴分别交于A、D两点,已知∠OBA=30°,点A的坐标为(2,O).