��Ŀ����
2��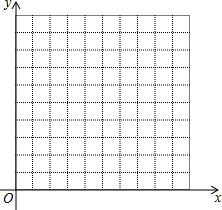 ��ƽ��ֱ������ϵ�У���A��ԭ��O������ÿ�������ƶ�2����λ���Ȼ������ƶ�1����λ���ȣ�
��ƽ��ֱ������ϵ�У���A��ԭ��O������ÿ�������ƶ�2����λ���Ȼ������ƶ�1����λ���ȣ���1��ʵ�������
��ƽ��ֱ������ϵ�������A�ӵ�O�������ƶ�1�κ�2�κ�3�κ���ܵ���ĵ㣬������Ӧ���������д�ڱ����У�
| A�ӵ�O�����ƶ����� | ���ܵ���ĵ������ |
| 1�� | ��0��2������1��0�� |
| 2�� | ��0��4������1��2������2��0�� |
| 3�� | ��0��6������1��4������2��2������3��0�� |
��һ���ƶ�����A���ܵ���ĵ�������ѧ����һ�ֺ�����ͼ���ϣ�
�����ƶ�1�κ��A���ܵ���ĵ�����ͼ��ĺ�������ʽ��
���ƶ�2�κ��ں���y=-2x+4��ͼ���ϣ����ɴ�����֪�����ƶ�n�κ��ں���y=-2x+2n��ͼ���ϣ�������д��Ӧ�ĺ�������ʽ��
��3��̽�����ã�
��A�ӵ�O��������n���ƶ�����ֱ��y=x�ϵĵ�B����ƽ�Ƶ���·����Ϊ20�����B�����꣮
���� ��1�����ݵ��ƽ���ص����ÿ��ƽ�ƺ�P���λ�ü��ɣ�
��2�����ȸ���P��ƽ��һ�κ�ĵ������������˵�ĺ�������ʽ�����ٸ��ݺ���ͼ��ƽ�Ƶ����ʽ�ɣ�
��3�����B������Ϊ��x��y�������B������꣬�ó�n�ķ��̣��ٸ��ݵ�B������Ϊ���������ɽ��н��
��� �⣺��1����ͼ��ʾ��
| P�ӵ�O����ƽ�ƴ��� | ���ܵ���ĵ� ������ |
| 1�� | ��0��2������1��0�� |
| 2�� | ��0��4������1��2������2��0�� |
| 3�� | ��0��6������1��4������2��2������3��0�� |
��$\left\{\begin{array}{l}{b=2}\\{k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=2}\\{k=-2}\end{array}\right.$��
�ʵ�һ��ƽ�ƺ�ĺ�������ʽΪ��y=-2x+2��
���ƶ�2�κ��ں���y=-2x+4��ͼ���ϣ����ɴ�����֪�����ƶ�n�κ��ں���y=-2x+2n��ͼ����
��3�����B��������x��y������������$\left\{\begin{array}{l}{y=-2x+2n}\\{y=x}\end{array}\right.$��
����������飬�õ���B������Ϊ��$\frac{2}{3}$n��$\frac{2}{3}$n����
��ƽ�Ƶ�·����Ϊx+y��
��$\frac{2}{3}$n+$\frac{2}{3}$n=20��
��n=15��
���B��������10��10����
���� ���⿼�����һ�κ�����ͼ���뼸�α任����֪����ͼ��ƽ�Ƶķ����ǽ�����Ĺؼ���

��ϰ��ϵ�д�
 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
�����Ŀ
11�� 1883�꣬���ж������������Σ��������ж������������ϵ�λ�����߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿһ�����µ�����֮һ�߶���ȡ�����м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ�����㼯�ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��n����ʱ�����µ������߶εij���֮��Ϊ��������
1883�꣬���ж������������Σ��������ж������������ϵ�λ�����߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿһ�����µ�����֮һ�߶���ȡ�����м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ�����㼯�ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��n����ʱ�����µ������߶εij���֮��Ϊ��������
 1883�꣬���ж������������Σ��������ж������������ϵ�λ�����߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿһ�����µ�����֮һ�߶���ȡ�����м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ�����㼯�ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��n����ʱ�����µ������߶εij���֮��Ϊ��������
1883�꣬���ж������������Σ��������ж������������ϵ�λ�����߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿһ�����µ�����֮һ�߶���ȡ�����м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ�����㼯�ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��n����ʱ�����µ������߶εij���֮��Ϊ��������| A�� | $\frac{2n}{3}$ | B�� | $\frac{2n}{3}$ | C�� | ${��\frac{2}{3}��^n}$ | D�� | ${��\frac{2}{3}��^{n-1}}$ |
 ��ͼ��ʾ��AB=AC=AD����˵����
��ͼ��ʾ��AB=AC=AD����˵����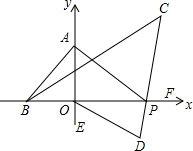 ��ͼ����ƽ��ֱ������ϵ�У���ABO=2��BAO��PΪx��������һ���㣬BCƽ�֡�ABP��PCƽ�֡�APF��ODƽ�֡�POE
��ͼ����ƽ��ֱ������ϵ�У���ABO=2��BAO��PΪx��������һ���㣬BCƽ�֡�ABP��PCƽ�֡�APF��ODƽ�֡�POE ��ͼ��ʾ����ij��˾һ������ԡ��ˮ���ˮ��y�������빩ˮʱ��x���֣��ĺ�����ϵ��
��ͼ��ʾ����ij��˾һ������ԡ��ˮ���ˮ��y�������빩ˮʱ��x���֣��ĺ�����ϵ��