题目内容
3.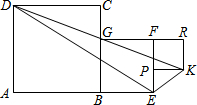 正方形ABCD,正方形BEFG和正方形PKRF的位置如图所示,点G在线段DK上,正方形BEFG的边长为2,则△DEK的面积为( )
正方形ABCD,正方形BEFG和正方形PKRF的位置如图所示,点G在线段DK上,正方形BEFG的边长为2,则△DEK的面积为( )| A. | 4 | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
分析 连DB,GE,FK,则DB∥GE∥FK,再根据正方形BEFG的边长为2,可求出S△DGE=S△GEB,S△GKE=S△GFE,再由SDEK=S正方形GBEF,即可求出答案.
解答 解:连接DB,GE,FK,则DB∥GE∥FK,
在梯形GDBE中,S△DGE=S△GEB(同底等高的两三角形面积相等),
同理S△GKE=S△GFE.
∴SDEK=S△DGE+S△GKE
=S△GEB+S△GEF
=S正方形GBEF
=2×2
=4.
故选A.
点评 此题主要考查正方形的性质,三角形和正方形面积公式以及梯形的性质,结合图形巧妙转化解决问题.

练习册系列答案
相关题目
11.用放大镜将图形放大,应属于哪一种变换( )
| A. | 对称变换 | B. | 平移变换 | C. | 旋转变换 | D. | 相似变换 |
18.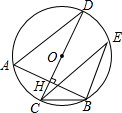 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
12.将抛物线y=x2+5向右平移1个单位长度,再向下平移2个单位长度,后,得到的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=(x+1)2-3 | D. | y=(x-1)2-3 |
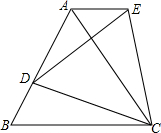 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.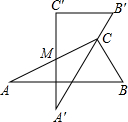 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5. 如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.
如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.