题目内容
13.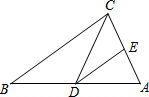 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )| A. | △ADE∽△ABC | B. | △ADE∽△ACD | C. | △DEC∽△CDB | D. | △ADE∽△DCB |
分析 由相似三角形的判定方法得出A、B、C正确,D不正确;即可得出结论.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,∠BCD=∠CDE,∠ADE=∠B,∠AED=∠ACB,
∵∠DCE=∠B,
∴∠ADE=∠DCE,
又∵∠A=∠A,
∴△ADE∽△ACD;
∵∠BCD=∠CDE,∠DCE=∠B,
∴△DEC∽△CDB;
∵∠B=∠ADE,
但是∠BCD<∠AED,且∠BCD≠∠A,
∴△ADE与△DCB不相似;
正确的判断是A、B、C,错误的判断是D;
故选:D.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,由两角相等得出三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.二次函数y=2(x-1)2+3的图象的顶点坐标是( )
| A. | (-2,3) | B. | (2,3) | C. | (1,-3) | D. | (1,3) |
3.小于1997且大于-1996的所有整数的和是( )
| A. | 1 | B. | -1995 | C. | 1996 | D. | 1997 |
 如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
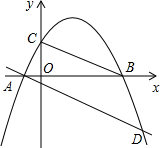 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.