题目内容
9.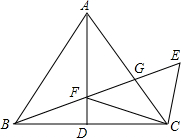 如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证:
如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证:(1)BF=CF;
(2)BF2=FG•FE.
分析 (1)根据等腰三角形的性质和线段垂直平分线的性质即可得到结论;
(2)根据等腰三角形的性质得到∠DBF=∠DCF,∠ABD=∠ACD,求得∠ABF=∠GCF;由平行线的性质得到∠ABF=∠CEF,推出△CFG∽△ECF,得到$\frac{FG}{CF}$=$\frac{CF}{EF}$,于是得到结论.
解答 证明:(1)∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴BF=CF;
(2)∵BF=CF,AB=AC,
∴∠DBF=∠DCF,∠ABD=∠ACD,
∴∠ABF=∠GCF;
∵CE∥AB,
∴∠ABF=∠CEF,
∴∠GCF=∠CEF,而∠GFC=∠CFE,
∴△CFG∽△ECF,
∴$\frac{FG}{CF}$=$\frac{CF}{EF}$,即CF2=FG•FE,
∴BF2=FG•FE.
点评 本题考查了等腰三角形的性质,线段垂直平分线的性质,相似三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
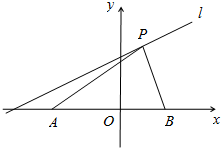 已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.
已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.

 如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?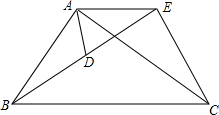 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.