题目内容
5．在△ABC中，延长BC到D，使CD=AC，连接AD，CE平分∠ACB交AB于E，且AE=BE，求证：BC=CD．分析 画出图形，根据三线合一判定等腰三角形，再利用等腰三角形的两腰相等证明即可．
解答 解：如图，
∵CE平分∠ACB交AB于E，且AE=BE，
∴△ACB是等腰三角形，
∴BC=AC，
∵CD=AC，
∴BC=CD．
点评 此题考查等腰三角形的判定，关键是根据三线合一判定等腰三角形，再利用等腰三角形的性质证明．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，在边长为1个单位长度的小正方形网格中：
16．
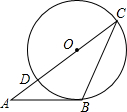如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B．如果∠A=34°，那么∠C等于（ ）
如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B．如果∠A=34°，那么∠C等于（ ）| A． | 28° | B． | 33° | C． | 34° | D． | 56° |
已知，如图，AB=CD，∠PAB的面积等于△PCD的面积，求证：OP平分∠BOD．
如图，在平行四边形ABCD中，AB=8，AD=6，∠DAB=30°，E、F是对角线AC的三等分点，则△BEF的面积是4．