题目内容
20.解不等式组:(1)$\left\{\begin{array}{l}{x-3(x-1)≤7}\\{1-\frac{2-5x}{3}<x}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x-\frac{3}{2}(2x-1)≤4}\\{\frac{1+3x}{2}>2x-1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{2x-7<5-2x}\\{x+1>\frac{3+x}{2}}\end{array}\right.$.
分析 先求出两个不等式的解集,再求其公共解.
解答 解:(1)$\left\{\begin{array}{l}{x-3(x-1)≤7①}\\{1-\frac{2-5x}{3}<x②}\end{array}\right.$,
由①得,x≥-2,
由②得,x<-$\frac{1}{2}$,
所以,不等式组的解集是-≤x<-$\frac{1}{2}$.
(2)$\left\{\begin{array}{l}{x-\frac{3}{2}(2x-1)≤4①}\\{\frac{1+3x}{2}>2x-1②}\end{array}\right.$,
由①得,x≥-$\frac{5}{4}$,
由②得,x<3,
所以,不等式组的解集是-$\frac{5}{4}$≤x<3.
(3)$\left\{\begin{array}{l}{2x-7<5-2x①}\\{x+1>\frac{3+x}{2}②}\end{array}\right.$,
由①得,x<3,
由②得,x>1,
所以,不等式组的解集是1<x<3.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
11. 如图,同心圆O中,大圆半径OA、OB分别交小圆于D、C,OA⊥OB,若四边形ABCD的面积为50,则图中阴影部分的面积为( )
如图,同心圆O中,大圆半径OA、OB分别交小圆于D、C,OA⊥OB,若四边形ABCD的面积为50,则图中阴影部分的面积为( )
 如图,同心圆O中,大圆半径OA、OB分别交小圆于D、C,OA⊥OB,若四边形ABCD的面积为50,则图中阴影部分的面积为( )
如图,同心圆O中,大圆半径OA、OB分别交小圆于D、C,OA⊥OB,若四边形ABCD的面积为50,则图中阴影部分的面积为( )| A. | 75 | B. | 50π | C. | 75π | D. | 75$\sqrt{2}$ |
10.下列运算正确的是( )
| A. | 2x2+3x3=5x5 | B. | (x+2)2=x2+4 | C. | x2•3x3=3x6 | D. | x6÷x3=x3 |
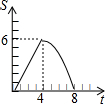
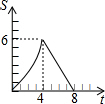
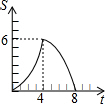
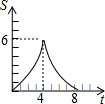
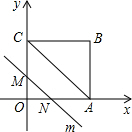 在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )