题目内容
17.在Rt△ABC中,∠C=90°,AB=8,cosA=$\frac{3}{4}$,求AC,BC的长.分析 根据余弦的概念列出算式,根据勾股定理计算得到答案.
解答 解:cosA=$\frac{AC}{AB}$=$\frac{3}{4}$,AB=8,
∴AC=6,
根据勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{7}$.
点评 本题考查的是解直角三角形的知识,掌握锐角三角函数的概念是解题的关键,注意勾股定理的正确运用.

练习册系列答案
相关题目
7.已知抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,其中A(-1,0)点D是抛物线y=$\frac{1}{2}$x2+bx-2的顶点,点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是( )
| A. | $\frac{25}{40}$ | B. | $\frac{24}{41}$ | C. | $\frac{23}{40}$ | D. | $\frac{25}{41}$ |
6.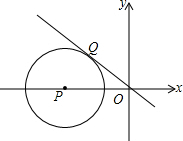 如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )
如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )
 如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )
如图,⊙P是圆心P(-$\sqrt{2}$,0),正比例函数y=-x的图象与⊙P相切于点Q,则Q点的坐标为( )| A. | (-1,1) | B. | ($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
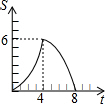
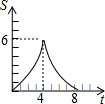
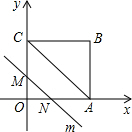 在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )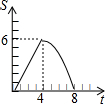
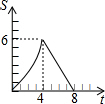
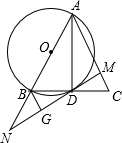 如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.
如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.