题目内容
17.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,….将以上三个等式两边分别相加得:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$.
(1)猜想并写出:$\frac{1}{{n({n+1})}}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)直接写出下列各式的计算结果:
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=$\frac{2016}{2017}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{{n×({n+1})}}$=$\frac{n}{n+1}$.
(3)探究并计算:$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$.
分析 根据题中给出的规律即可化简求值;
解答 解:(1)由题意可知:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{2016}$-$\frac{1}{2017}$)
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$,
②原式═(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$,
(3)∵$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)
原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$)+$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$)+…$\frac{1}{2}$($\frac{1}{2014}$-$\frac{1}{2016}$)
=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2016}$)
=$\frac{1007}{4032}$,
故答案为:(1)$\frac{1}{n}-\frac{1}{n+1}$;(2)①$\frac{2016}{2017}$;②$\frac{n}{n+1}$;
点评 本题考查数字规律,注意利用题中所给的规律.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | -1、0、-1 | B. | 无、1、0 | C. | -1、1、0 | D. | 均无 |
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
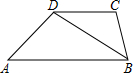 如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.
如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.