题目内容

7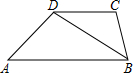．如图所示，在梯形ABCD中，AB∥CD，BD2=AB•DC，求证：∠A=∠CBD．

分析 先根据AB∥CD得出∠BDC=∠ABD，再由BD2=AB•DC得出$\frac{AB}{BD}$=$\frac{BD}{DC}$，故可得出△ABD∽△BDC，由此可得出结论．

解答 证明：∵AB∥CD，
∴∠BDC=∠ABD．
∵BD2=AB•DC，
∴$\frac{AB}{BD}$=$\frac{BD}{DC}$，
∴△ABD∽△BDC，
∴∠A=∠CBD．

点评 本题考查的是相似三角形的判定与性质，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．

练习册系列答案
相关题目
17．观察下列等式：$\frac{1}{1×2}$=1-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，…．
将以上三个等式两边分别相加得：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$．
（1）猜想并写出：$\frac{1}{{n（{n+1}）}}$=$\frac{1}{n}$-$\frac{1}{n+1}$．
（2）直接写出下列各式的计算结果：
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=$\frac{2016}{2017}$；
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{{n×（{n+1}）}}$=$\frac{n}{n+1}$．
（3）探究并计算：$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$．
18．解方程：
（1）（2x+3）2-16=0；                  
（2）x2+4x-4=0（用配方法）
（3）（x-3）2-2x（x-3）=0；                
（4）3y2+4y-4=0．
15．已知：x=$\sqrt{2}$+1，y=$\sqrt{2}$-1，求下列各式的值：
（1）x2-y2
（2）x2+2xy+y2．
2．尝试练习：
（1）$\frac{3b}{x}$+$\frac{b}{x}$                                     
（2）$\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$      
（3）$\frac{2y}{x-1}$-$\frac{3y+1}{1-x}$-$\frac{y}{x-1}$                 
（4）$\frac{6x}{5x-7}$-$\frac{3x-8}{7-5x}$+$\frac{-x+6}{7-5x}$．
12．5x-2x=-9，则x=-3．
19．“鸡兔同笼”是我国民间流传的诗歌形式的数学题：“鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几多鸡儿几多兔”解决此问题，可设鸡有x只，则所列方程的是（　　）
A．x+2（36+x）=100B．4x+2（36-x）=100C．2x+4（36-x）=100D．2x+2（36-x）=100
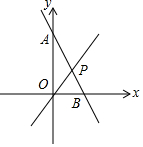16．如图，已知一条直线经过点A（0，4）、点B（2，0）．
（1）若点P是线段AB的中点，求直线OP的解析式；
（2）将这条直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D，使DB=DC，求：直线CD的函数解析式．
19．如图，已知∠1=∠2，∠3=50°，求∠4的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网